U2L4-2——向量加减乘除

Vector3的相互计算

Vector3基础里已经包含了Vector3基本计算
这里将详细讲解它们的几何意义

1. 向量加法 —— 主要用于位置平移和向量计算
2. 向量减法 —— 主要用于位置平移和向量计算
3. 向量乘除法 —— 主要用于模长放大缩小

向量加法

向量A：(Xa,Ya,Za)
向量B：(Xb,Yb,Zb)
A + B = (Xa + Xb, Ya + Yb, Za + Zb)

this.transform.position += new Vector3(1, 2, 3);

Vector3+Vector3的意义

1. 位置+位置 几何意义：
   两个位置相加没有任何意义

2. 向量+向量 几何意义：
   两个向量相加得到一个新向量
   向量 + 向量 = 向量
   口诀： 向量相加，首尾相连

​​

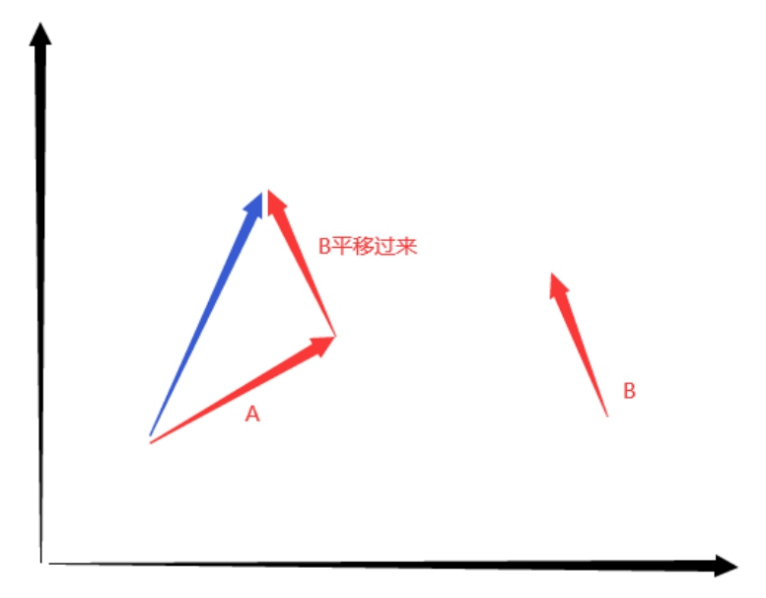
3. 位置+向量 几何意义：
   位置加向量得到一个新位置
   位置 + 向量 = 位置
   向量 + 位置 = 位置
   口诀： 位置和向量相加=平移位置

​​

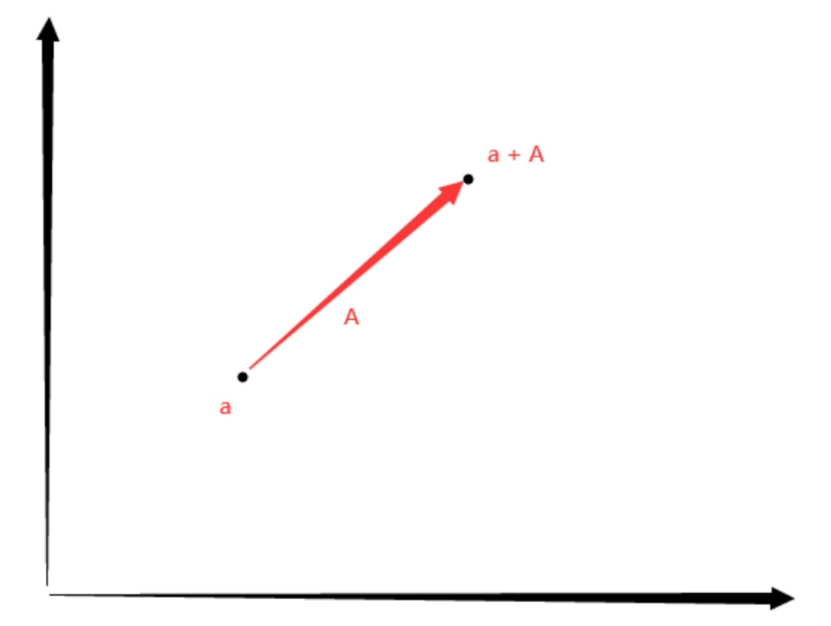
向量减法

向量A(Xa,Ya,Za)
向量B(Xb,Yb,Zb)
A - B = (Xa - Xb, Ya - Yb, Za - Zb)

this.transform.position -= new Vector3(1, 2, 3);

Vector3-Vector3的意义

1. 位置-位置 几何意义：
   两个位置相减得到一个新向量
   位置 - 位置 = 向量
   口诀：两点决定一向量，终点 - 起点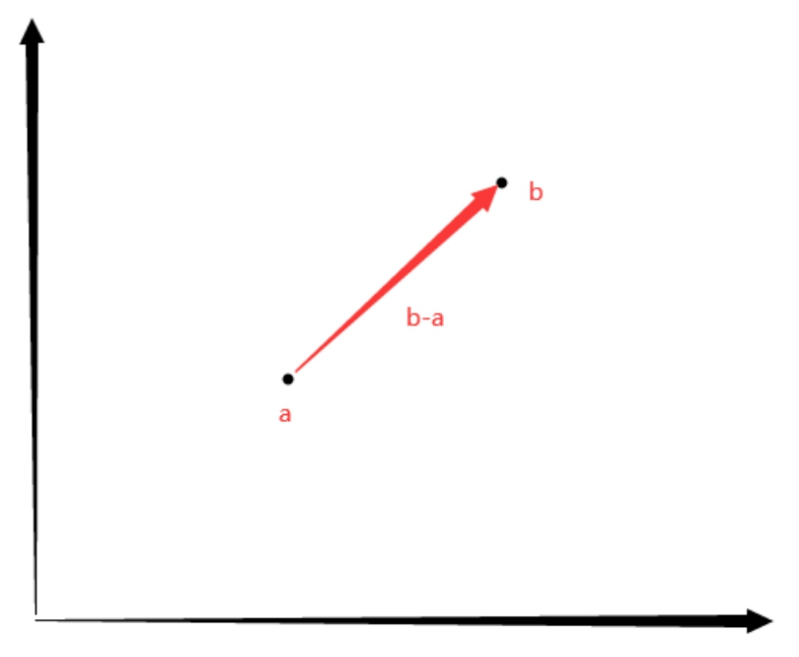

   ​​

2. 向量-向量 几何意义：
   两个向量相减得到一个新向量
   向量 - 向量 = 向量
   口诀：向量相减，头连头，尾指尾，A - B = B头指A头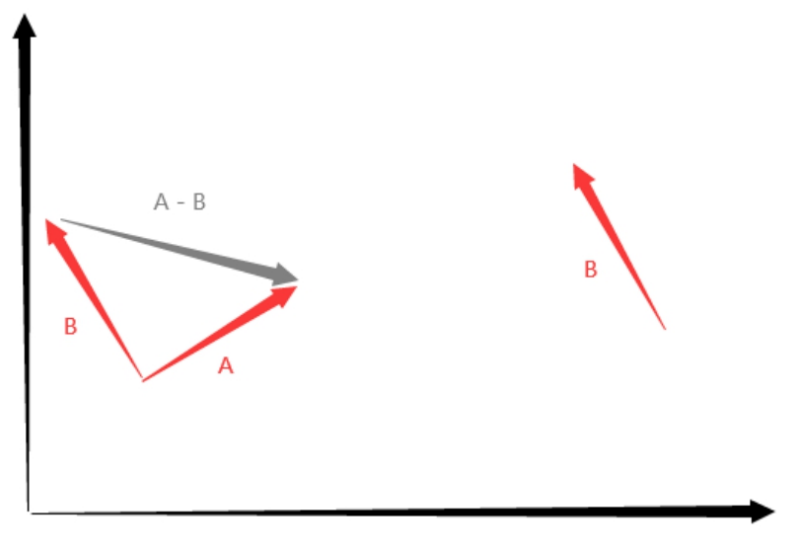

   ​​

3. 位置-向量 几何意义：
   位置减向量 相当于 加负向量
   位置 + (-向量) = 位置
   口诀：位置减向量 = 平移位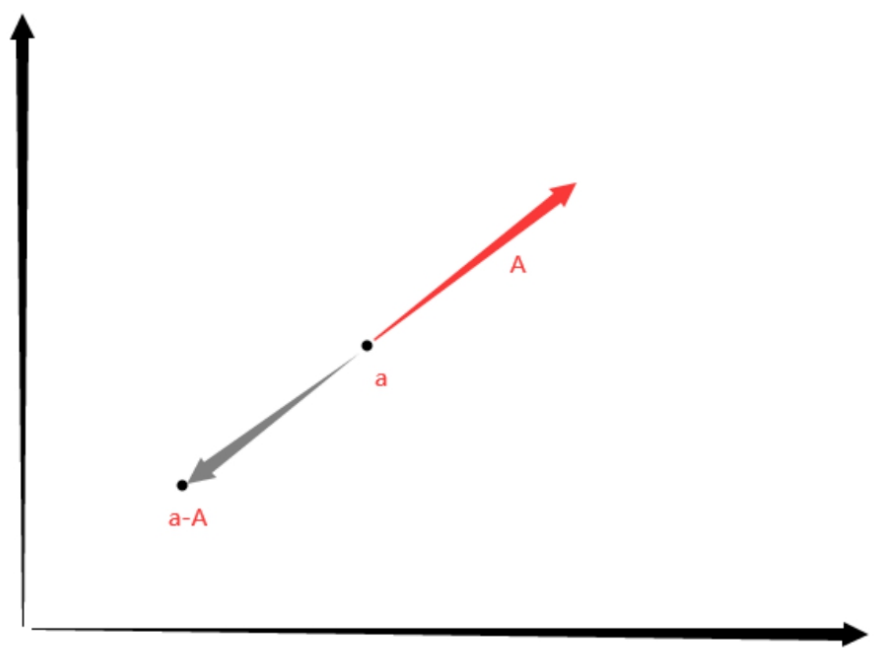

   ​​

4. 向量-位置 几何意义：
   向量减位置没有任何意义

向量乘除

向量只会和标量进行乘除法运算
向量A(x,y,z)
标量a
​$A * a = (x * a, y * a, z * a)$
​$A/a = (x/a,y/a,z/a)$

this.transform.localScale *= 2;
this.transform.localScale /= 2;

向量和标量乘除的 几何意义

• 向量 * or / 标量 = 向量
• 向量 * or / 正数，方向不变，放大缩小模长
• 向量 * or / 负数，方向相反，放大缩小模长
• 向量 * 0，得到零向量