U2L4-3——向量点乘

向量点乘

向量点乘可以用来判断对象的方位，计算两个向量之间的夹角

点乘计算公式：
向量A:(Xa,Ya,Za)A:(X_a,Y_a,Z_a)
向量B:(Xb,Yb,Zb)B:(X_b,Y_b,Z_b)

A⃗⋅B⃗=Xa×Xb+Ya×Yb+Za×Zb=∣A⃗∣∣B⃗∣cos⁡θ\vec{A} \cdot \vec{B} = X_a \times X_b + Y_a \times Y_b + Z_a \times Z_b = |\vec{A}||\vec{B}|\cos\theta

向量 · 向量 = 标量

向量点乘的几何意义是：
一个向量到另一个向量的投影的长度
点乘结果 > 0 两个向量夹角为锐角
点乘结果 = 0 两个向量夹角为直角
点乘结果 < 0 两个向量夹角为钝角
我们可以用这个规律判断对方的大致方位

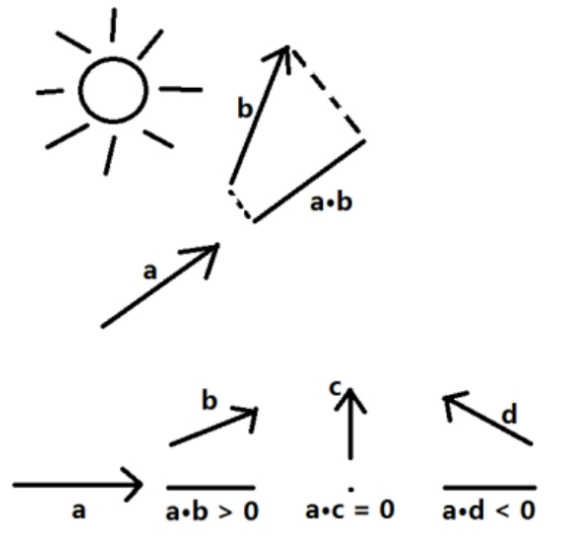
​image​

它与向量模长和单位向量知识延伸出：
如果向量和自己的点乘结果为1，则该向量为单位向量：A⋅A=x2+y2+z2=1A \cdot A = x^2+y^2+z^2=1

值得一提的是，两个标准化后的单位向量，点乘以后得到的是这两个单位向量夹角的 cos⁡\cos 值

本章代码关键字

1
2
3
4
Debug.DrawLine(, , )    //调试的画线段方法
Debug.DrawRay(, , )    //调试的画射线方法
Vector3.Dot(,)        //计算两个向量点乘结果的方法
Vector3.Angle(,)    //得到两个向量之间夹角的方法

调试画线

画线段

前两个参数 分别是 起点 终点

1
2
//前两个参数 分别是 起点 终点
Debug.DrawLine(this.transform.position, this.transform.position + this.transform.forward, Color.red);

画射线

前两个参数 分别是 起点 方向

1
2
//前两个参数 分别是 起点 方向
Debug.DrawRay(this.transform.position, this.transform.forward, Color.white);

计算两个向量点乘方法

Vector3 提供了计算点乘的方法 (向量点乘)

1
2
//Vector3 提供了计算点乘的方法
float dotResult = Vector3.Dot(this.transform.forward, target.position - this.transform.position);

通过点乘判断对方方位

1
2
3
4
5
6
7
8
9
10
11
//得到两个向量的点乘结果
//向量 a 点乘 AB 的结果
float dotResult = Vector3.Dot(this.transform.forward, target.position - this.transform.position);
if (dotResult < 0)    //两向量夹角为钝角
{
    print("在我后方");
}
else            //两向量夹角为锐角
{
    print("在我前方");
}

通过点乘推导公式算出夹角

重要推论：AB夹角 = Acos(单位向量A · 单位向量B)
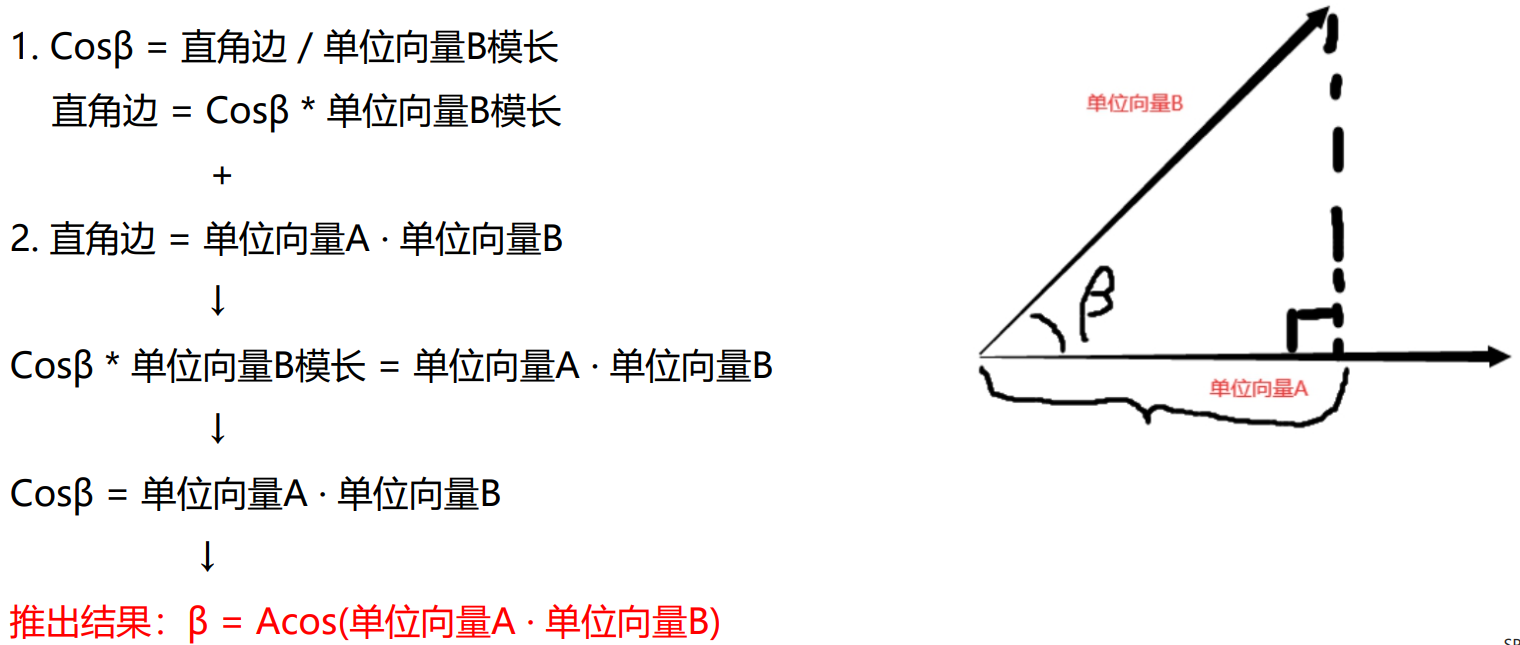
​image​

步骤

  1. 用单位向量算出点乘结果
  2. 用反三角函数得出角度
1
2
3
4
5
//步骤
//1、用单位向量算出点乘结果
dotResult = Vector3.Dot(this.transform.forward, (target.position - this.transform.position).normalized);
//2、用反三角函数得出角度
print("角度：" + Mathf.Acos(dotResult) * Mathf.Rad2Deg);

得到两个向量之间夹角的方法

​Vector3​也提供了 得到两个向量之间夹角的方法(返回的是角度，和Mathf​​不同！！！)

1
print("角度2：" + Vector3.Angle(this.transform.forward, target.position - this.transform.position));