U2L4-4——向量叉乘
U2L4-4——向量叉乘
向量叉乘
向量×向量
向量A (Xa,Ya,Za)
向量B (Xb,Yb,Zb)
A x B = (X,Y,Z)
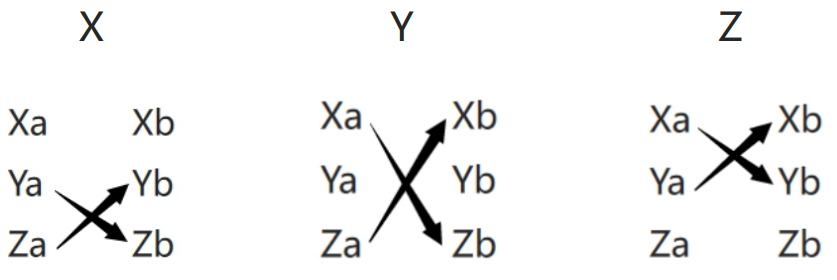
X = YaZb - ZaYb
Y = ZaXb - XaZb
Z = XaYb - YaXb
A x B 得到的向量同时垂直A和B
A x B 向量垂直于A和B
组成的平面 A x B = -(B x A)
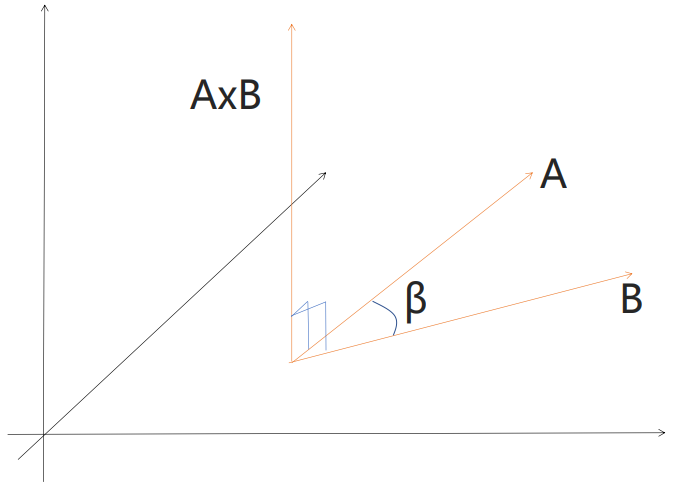
向量叉乘的几何意义是:
假设向量 A和B 都在XZ平面上
向量A 叉乘 向量B
结果大于0 说明 B在A右侧
结果小于0 说明 B在A左侧这个左侧右侧的判定标准是以OA向量方向为准
向量叉乘对于我们的意义
- 得到一个平面的法向量
- 得到两个向量之间的左右位置关系
注意!叉乘左右两边向量如果互换位置结果会变为原来的负向量,因此切记要确定叉乘的左向量和右向量
本章代码关键字
1 | Vector3.Cross(, ) //计算两个向量叉乘的方法 |
叉乘计算
Vector3提供了叉乘的方法(向量叉乘)
1 | print(Vector3.Cross(A.position, B.position)); |
用向量叉乘判断目标在左侧还是右侧
1 | Vector3 C = Vector3.Cross(A.position, B.position); |
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来源 文KRIFE齐的博客!
