U2L4-0——Vector3向量必备知识

向量相关知识

  • 标量：只有数值大小而没有方向
  • 向量：有数值大小且有方向的矢量，向量有一维，二维，三维等

在数学中，向量（也称为欧几里得向量、几何向量），指具有大小（magnitude）和方向的量。
它可以形象化地表示为带箭头的线段。
箭头所指：代表向量的方向；线段长度：代表向量的大小。与向量对应的量叫做数量（物理学中称标量），数量（或标量）只有大小，没有方向。

向量（数学用语）_百度百科 (baidu.com)

向量在空间中的表示

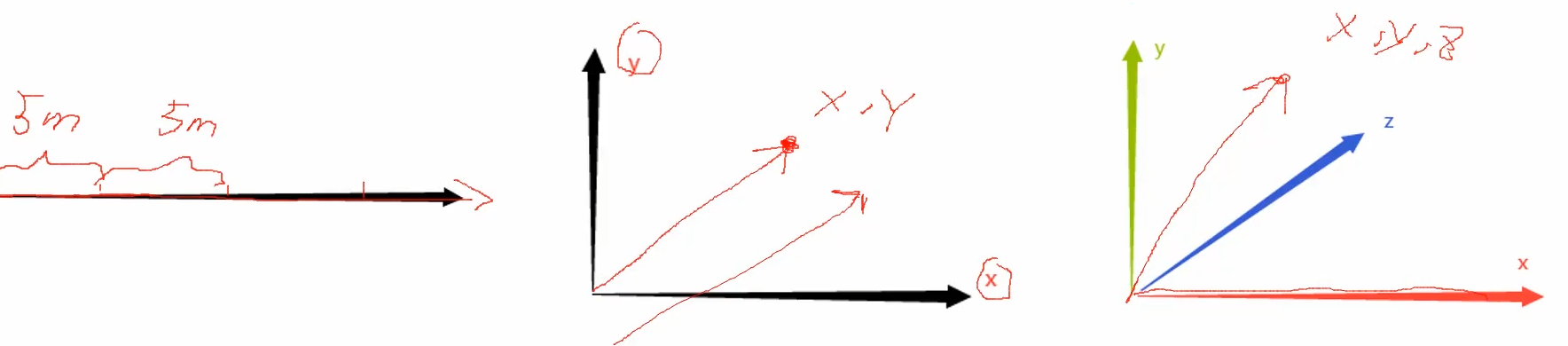
​image​

注意：向量在空间中有无数条可以随意移动

Vector3向量的含义

Vector3类型的变量 可以表示一个点 也可以表示一个向量 具体表示什么 是根据我们的具体需求和逻辑决定
如何在Unity里面得到向量 终点减起点 就可以得到向量 C也可以代表向量 代表的是OC向量 O是坐标系原点

Vector3有两种几何含义：

  1. 位置 —— 代表一个点
  2. 方向 —— 代表一个方向向量
1
2
3
4
5
//1、位置 —— 代表一个点
print(this.transform.position);
//2、方向 —— 代表一个方向向量
print(this.transform.forward);
print(this.transform.up);
1
2
3
4
5
//三维向量
Vector3 v = new Vector3(1, 2, 3);
//二维向量
Vector3 v2 = new Vector3(1, 2);
//一维向量，基本可以视为标量

两点决定一个向量

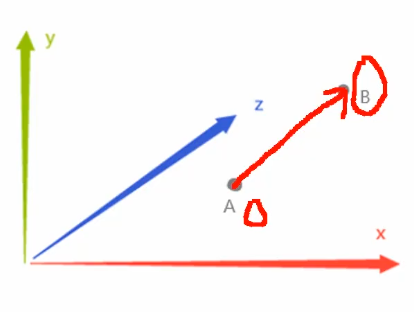
​image​

A点：(Xa,Ya,Za)
B点：(Xb,Yb,Zb)
从A指向B的向量为AB向量
B-A = (Xb-Xa,Yb-Ya,Zb-Za)
A-B = (Xa-Xb,Ya-Yb,Za-Zb)
口诀：终点减起点

1
2
3
4
5
6
7
//A和B此时几何意义是两个点
Vector3 A = new Vector3(1, 2, 3);
Vector3 B = new Vector3(5, 1, 5);
//求向量
//此时 AB和BA此时的几何意义是两个向量
Vector3 AB = B - A;
Vector3 BA = A - B;

零向量

就是（0，0，0）的向量，零向量是唯一一个大小为0的向量

1
2
//零向量
print(Vector3.zero);

负向量

(x,y,z)的负向量为(-x,-y,-z)
负向量和原向量大小相等
负向量和原向量方向相反

1
2
3
//负向量
print(Vector3.forward);
print(-Vector3.forward);