US2S1L3——特殊矩阵

特殊矩阵

  1. 方块矩阵 —— 行列数相等的矩阵

  2. 对角矩阵 —— 只有主对角线有值，其余元素全为零的 方阵

  3. 单位矩阵 —— 主对角线上的元素均为1 的 对角矩阵

  4. 数量矩阵 —— 主对角线上的元素为同一值 的 对角矩阵

  5. 转置矩阵 —— 将原始矩阵的行和列互换得到的 新矩阵

    1. 矩阵转置的转置等于原矩阵 (MT)T=M(M^T)^T = M
    2. 矩阵串接的转置，等于反向串接各个矩阵的转置 (AB)T=BTAT(AB)^T =B^TA^T

  6. 逆矩阵 —— MM−1=M−1M=I（单位矩阵）MM^{−1} = M^{−1}M = I（单位矩阵）

  7. 正交矩阵 —— 一个方阵和它的转置矩阵相乘为单位矩阵，那么它就是正交矩阵：MMT=MTM=IMM^T = M^TM = I

  8. 列矩阵和行矩阵 —— 列矩阵就是只有一列的矩阵；行矩阵就是只有一行的矩阵。他们一般用于表示向量

方块矩阵

方块矩阵简称方阵，它的特点是**行列数相等**，比如 3×33\times3、4×44\times4，n×nn \times n 的矩阵都可以称为方阵

[2571][123654789][4578070532540122]\begin{bmatrix} 2 & 5 \\ 7 & 1 \\ \end{bmatrix} \qquad \begin{bmatrix} 1 & 2 & 3 \\ 6 & 5 & 4 \\ 7 & 8 & 9 \\ \end{bmatrix} \qquad \begin{bmatrix} 4 & 5 & 7 & 8 \\ 0 & 7 & 0 & 5 \\ 3 & 2 & 5 & 4 \\ 0 & 1 & 2 & 2 \\ \end{bmatrix}

对角矩阵

对角矩阵是一种特殊的方阵，它是 只有主对角线有值，其余元素全为零 的 方阵

[2001][100050009][4000070000500002]\begin{bmatrix} 2 & 0 \\ 0 & 1 \\ \end{bmatrix} \qquad \begin{bmatrix} 1 & 0 & 0 \\ 0 & 5 & 0 \\ 0 & 0 & 9 \\ \end{bmatrix} \qquad \begin{bmatrix} 4 & 0 & 0 & 0 \\ 0 & 7 & 0 & 0 \\ 0 & 0 & 5 & 0 \\ 0 & 0 & 0 & 2 \\ \end{bmatrix}

注意：矩阵中的主对角线就是指 从左上角到右下角的对角线

单位矩阵

单位矩阵是一种特殊的对角矩阵 它是 主对角线上的元素均为1 的 对角矩阵

[1001][100010001][1000010000100001]\begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix} \qquad \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} \qquad \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}

注意：任何矩阵(MM)和单位矩阵(II)相乘的结果都是原来的矩阵（前提是满足相乘的规则）

MI=IM=MMI = IM = M

[2341]×[1001]=[1001]×[2341]=[2341]\begin{bmatrix} 2 & 3 \\ 4 & 1 \\ \end{bmatrix} \times \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix} \times \begin{bmatrix} 2 & 3 \\ 4 & 1 \\ \end{bmatrix} = \begin{bmatrix} 2 & 3 \\ 4 & 1 \\ \end{bmatrix}

数量矩阵

数量矩阵是一种特殊的对角矩阵，它是 主对角线上的元素为同一值 的 对角矩阵

[7007][9.50009.50009.5][7000070000700007]\begin{bmatrix} 7 & 0 \\ 0 & 7 \\ \end{bmatrix} \qquad \begin{bmatrix} 9.5 & 0 & 0 \\ 0 & 9.5 & 0 \\ 0 & 0 & 9.5 \\ \end{bmatrix} \qquad \begin{bmatrix} 7 & 0 & 0 & 0 \\ 0 & 7 & 0 & 0 \\ 0 & 0 & 7 & 0 \\ 0 & 0 & 0 & 7 \\ \end{bmatrix}

数量矩阵和单位矩阵的关系：假设 II 是单位矩阵，kk是任何数，则 kIkI 称为数量矩阵

转置矩阵

转置矩阵是将 原始矩阵的行和列 互换得到的新矩阵，假设矩阵为 MM ，那 MM 的转置矩阵一般写为 MTM^T

[56976012]T=[56609172][125698]T=[159268]\begin{bmatrix} 5 & 6 & 9 & 7 \\ 6 & 0 & 1 & 2 \\ \end{bmatrix}^T = \begin{bmatrix} 5 & 6 \\ 6 & 0 \\ 9 & 1 \\ 7 & 2 \\ \end{bmatrix} \qquad \begin{bmatrix} 1 & 2 \\ 5 & 6 \\ 9 & 8 \\ \end{bmatrix}^T = \begin{bmatrix} 1 & 5 & 9 \\ 2 & 6 & 8 \\ \end{bmatrix}

[xyz]T=[xyz][xyz]T=[xyz]\begin{bmatrix} x & y & z \\ \end{bmatrix}^T = \begin{bmatrix} x \\ y \\ z \\ \end{bmatrix} \qquad \begin{bmatrix} x \\ y \\ z \\ \end{bmatrix}^T = \begin{bmatrix} x & y & z \\ \end{bmatrix}

转置矩阵对于我们来说有一些常用的性质

  1. 矩阵转置的转置等于原矩阵

    (MT)T=M(M^T)^T = M

  2. 矩阵串接的转置，等于反向串接各个矩阵的转置

    (AB)T=BT×AT(AB)^T =B^T \times A^T

逆矩阵

逆矩阵是所有特殊矩阵当中计算最复杂的矩阵
它的特点是 逆矩阵是必须是一个方阵，并且不是所有矩阵都有逆矩阵
假设 一个方阵 MM ， 它的逆矩阵用 M−1M^{−1} 表示
那么 MM−1=M−1M=I（单位矩阵）MM^{−1} = M^{−1}M = I（单位矩阵）

如果一个矩阵存在对应的逆矩阵，我们就说该矩阵是可逆的（或称非奇异的）
如果不存在，那么该矩阵为不可逆的（或称奇异的）

逆矩阵的计算

  1. 确定矩阵为方阵（即行列数相等）
  2. 计算矩阵的行列式（若行列式值为0，则该矩阵没有逆矩阵，也就是矩阵不可逆）
  3. 计算矩阵的代数余子式矩阵
  4. 计算标准伴随矩阵（转置代数余子式矩阵）
  5. 计算逆矩阵（标准伴随矩阵 / 行列式）

行列式的计算方式

假设矩阵为 MM，∣M∣|M| 表示 MM 矩阵的行列式，行列式是一个标量（数值）

计算口诀：
左下左上画对角，线上数值都相乘，
数值数量为行列，数量不够对岸取，
左下分组加，左上分组减

  • 2×22 \times 2 矩阵的行列式计算方式：

    [m11m12m21m22]=+m11×m22−+m21×m12\begin{align*} & \begin{bmatrix} m_{11} & m_{12} \\ m_{21} & m_{22} \end{bmatrix} \\ = & + m_{11} \times m_{22} - + m_{21} \times m_{12} \\ \end{align*}

    或者这样记：

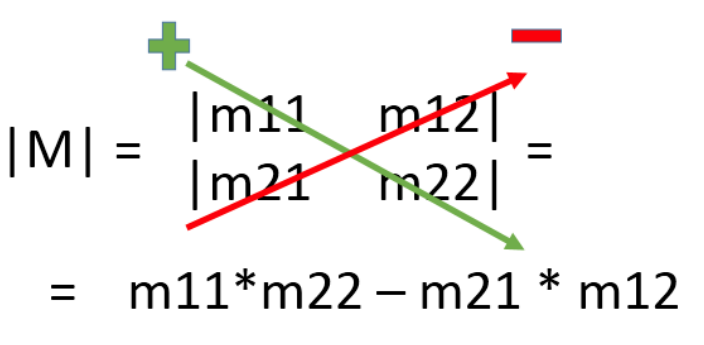
    ​image​

  • 3×33 \times 3 矩阵的行列式计算方式：

    [m11m12m13m21m22m23m31m32m33]=+m11×m22×m33+m21×m32×m13+m31×m12×m23−m31×m22×m13−m32×m23×m11−m33×m21×m12\begin{align*} & \begin{bmatrix} m_{11} & m_{12} & m_{13} \\ m_{21} & m_{22} & m_{23} \\ m_{31} & m_{32} & m_{33} \\ \end{bmatrix} \\ = & + m_{11} \times m_{22} \times m_{33} + m_{21} \times m_{32} \times m_{13} + m_{31} \times m_{12} \times m_{23} \\ & - m_{31} \times m_{22} \times m_{13} - m_{32} \times m_{23} \times m_{11} - m_{33} \times m_{21} \times m_{12} \end{align*}

    或者这样记：

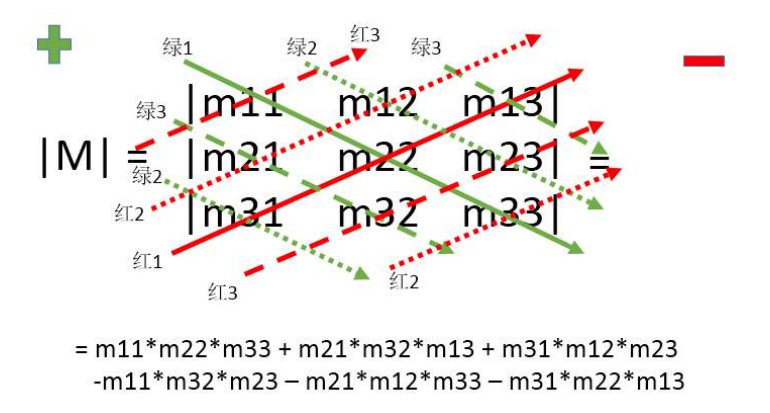
    ​image​

示例：

∣[43−32]∣=4×2−3×(−3)=8−(−9)=17\begin{align*} & \left | \begin{bmatrix} 4 & 3 \\ -3 & 2 \end{bmatrix} \right | \\ = & 4 \times 2 - 3 \times (-3) \\ = & 8 - (-9) \\ = & 17 \end{align*}

∣[1−233213−20]∣=+1×2×0+3×(−2)×3+3×(−2)×(−1)−3×2×3−3×(−2)×0−1×(−2)×(−1)=0+(−18)+6−18−0−2=−32\begin{align*} & \left | \begin{bmatrix} 1 & -2 & 3 \\ 3 & 2 & 1 \\ 3 & -2 & 0 \\ \end{bmatrix} \right | \\ = & + 1 \times 2 \times 0 + 3 \times (-2) \times 3 + 3 \times (-2) \times (-1) \\ & - 3 \times 2 \times 3 - 3 \times (-2) \times 0 - 1 \times (-2) \times (-1) \\ = & 0 + (-18) + 6 - 18 - 0 - 2 \\ = & -32 \end{align*}

代数余子式矩阵的计算方式

假设 矩阵 MM 的 代数余子式矩阵为 矩阵 CC

M=[m11m12m13m21m22m23m31m32m33]M = \begin{bmatrix} m_{11} & m_{12} & m_{13} \\ m_{21} & m_{22} & m_{23} \\ m_{31} & m_{32} & m_{33} \end{bmatrix}

C=[c11c12c13c21c22c23c31c32c33]C = \begin{bmatrix} c_{11} & c_{12} & c_{13} \\ c_{21} & c_{22} & c_{23} \\ c_{31} & c_{32} & c_{33} \end{bmatrix}

标量的代数余子式计算规则：Cij=−1的i+j次幂×去掉第i行，j列组成的矩阵的行列式C_{ij} = -1的i+j次幂 \times 去掉第i行，j列组成的矩阵的行列式

C11=−11+1×∣[m22m23m32m33]∣=−12×(m22⋅m33−m32⋅m23)C_{11}= -1^{1 + 1} \times \left | \begin{bmatrix} m_{22} & m_{23} \\ m_{32} & m_{33} \\ \end{bmatrix} \right | = -1^{2} \times (m_{22} \cdot m_{33} - m_{32} \cdot m_{23})

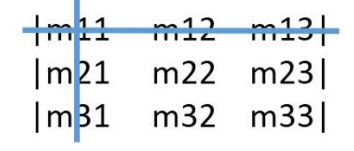
image

C12=−11+2×∣[m21m23m31m33]∣=−13×(m21⋅m33−m31⋅m23)C_{12}= -1^{1 + 2} \times \left | \begin{bmatrix} m_{21} & m_{23} \\ m_{31} & m_{33} \\ \end{bmatrix} \right | = -1^{3} \times (m_{21} \cdot m_{33} - m_{31} \cdot m_{23})

image

举例：

[1−2312−13−20]，其代数余子式矩阵C=[−2−3−12−6−9−4−4108]\begin{bmatrix} 1 & -2 & 3 \\ 1 & 2 & -1 \\ 3 & -2 & 0 \\ \end{bmatrix} ，其代数余子式矩阵C = \begin{bmatrix} -2 & -3 & -12 \\ -6 & -9 & -4 \\ -4 & 10 & 8 \\ \end{bmatrix}

​image​

标准伴随矩阵的计算方式

标准伴随矩阵 为原矩阵的 代数余子式矩阵 的转置矩阵
假设 矩阵 MM 的 代数余子式矩阵为 矩阵 CC

M=[m11m12m13m21m22m23m31m32m33]M = \begin{bmatrix} m_{11} & m_{12} & m_{13} \\ m_{21} & m_{22} & m_{23} \\ m_{31} & m_{32} & m_{33} \end{bmatrix}

C=[c11c12c13c21c22c23c31c32c33]C = \begin{bmatrix} c_{11} & c_{12} & c_{13} \\ c_{21} & c_{22} & c_{23} \\ c_{31} & c_{32} & c_{33} \end{bmatrix}

那么矩阵 MM 的标准伴随矩阵为

CT=[c11c21c31c12c22c32c13c23c33]C^T = \begin{bmatrix} c_{11} & c_{21} & c_{31} \\ c_{12} & c_{22} & c_{32} \\ c_{13} & c_{23} & c_{33} \end{bmatrix}

举例：

[1−2312−13−20]，其代数余子式矩阵C=[−2−3−12−6−9−4−4108]\begin{bmatrix} 1 & -2 & 3 \\ 1 & 2 & -1 \\ 3 & -2 & 0 \\ \end{bmatrix} ，其代数余子式矩阵C = \begin{bmatrix} -2 & -3 & -12 \\ -6 & -9 & -4 \\ -4 & 10 & 8 \\ \end{bmatrix}

因此，它的标准伴随矩阵为CTC^T：

CT=[−2−6−4−3−910−12−48]C^T = \begin{bmatrix} -2 & -6 & -4 \\ -3 & -9 & 10 \\ -12 & -4 & 8 \\ \end{bmatrix}

计算逆矩阵

逆矩阵 为 标准伴随矩阵 / 行列式

标准伴随矩阵为

[1−2312−13−20]，其代数余子式矩阵C=[−2−3−12−6−9−4−4108]，其标准伴随矩阵为CT=[−2−6−4−3−910−12−48]\begin{bmatrix} 1 & -2 & 3 \\ 1 & 2 & -1 \\ 3 & -2 & 0 \\ \end{bmatrix} ，其代数余子式矩阵C = \begin{bmatrix} -2 & -3 & -12 \\ -6 & -9 & -4 \\ -4 & 10 & 8 \\ \end{bmatrix} ，其标准伴随矩阵为C^T = \begin{bmatrix} -2 & -6 & -4 \\ -3 & -9 & 10 \\ -12 & -4 & 8 \\ \end{bmatrix}

行列式为

∣[1−233213−20]∣=+1×2×0+3×(−2)×3+3×(−2)×(−1)−3×2×3−3×(−2)×0−1×(−2)×(−1)=0+(−18)+6−18−0−2=−32\begin{align*} & \left | \begin{bmatrix} 1 & -2 & 3 \\ 3 & 2 & 1 \\ 3 & -2 & 0 \\ \end{bmatrix} \right | \\ = & + 1 \times 2 \times 0 + 3 \times (-2) \times 3 + 3 \times (-2) \times (-1) \\ & - 3 \times 2 \times 3 - 3 \times (-2) \times 0 - 1 \times (-2) \times (-1) \\ = & 0 + (-18) + 6 - 18 - 0 - 2 \\ = & -32 \end{align*}

因此，它的逆矩阵为

M−1=CT−32=[−2−32−6−32−4−32−3−32−9−3210−32−12−32−4−328−32]=[11631618332932−5163818−14]M^{-1} = \frac{C^T}{-32} = \begin{bmatrix} \frac{-2}{-32} & \frac{-6}{-32} & \frac{-4}{-32} \\ \frac{-3}{-32} & \frac{-9}{-32} & \frac{10}{-32} \\ \frac{-12}{-32} & \frac{-4}{-32} & \frac{8}{-32} \\ \end{bmatrix} = \begin{bmatrix} \frac{1}{16} & \frac{3}{16} & \frac{1}{8} \\ \frac{3}{32} & \frac{9}{32} & -\frac{5}{16} \\ \frac{3}{8} & \frac{1}{8} & -\frac{1}{4} \\ \end{bmatrix}

逆矩阵的重要性质

  1. 逆矩阵的逆矩阵是原矩阵本身 (M−1)−1=M(M^{-1})^{-1}=M

  2. 矩阵乘以自己的逆矩阵为单位矩阵 MM−1=M−1M=IMM^{-1}=M^{-1}M=I

  3. 单位矩阵的逆矩阵是它本身 I−1=II^{-1}=I

  4. 转置矩阵的逆矩阵是逆矩阵的转置 (MT)−1=(M−1)T(M^T)^{-1}=(M^{-1})^T

  5. 矩阵串接相乘后的逆矩阵 等于 反向串接各个矩阵的逆矩阵 相乘

    (AB)−1=B−1A−1(AB)^{-1}=B^{-1}A^{-1}

    (ABCD)−1=D−1C−1B−1A−1(ABCD)^{-1}=D^{-1}C^{-1}B^{-1}A^{-1}

  6. 逆矩阵可以计算矩阵变换的反向变换（ MM 为矩阵，vv 为一个矢量（向量））
    或者说，当一个矢量vv被一个矩阵MM变换（平移、旋转、缩放）时（MvMv），再左乘一个M−1M^{-1}即可将这个矢量vv变换回来

    M−1(Mv)=(M−1M)v=Iv=vM^{-1}(Mv)=(M^{-1}M)v=Iv=v

正交矩阵

前置知识：逆矩阵，向量点乘，向量模长和单位向量

正交矩阵是一种特殊的方阵，正交的意思是垂直
它的特点是：一个方阵和它的转置矩阵相乘为单位矩阵，那么它就是正交矩阵：MMT=MTM=IMM^T = M^TM = I

通过正交矩阵的这一性质，再根据上节课学习的逆矩阵的一个重要性质：MM−1=M−1M=IMM^{−1} = M^{−1}M = I

我们可以推导出：如果一个矩阵是正交的，那么它的逆矩阵等于其转置矩阵：MT=M−1M^T = M^{−1}
如果一个矩阵是正交矩阵，那么它的转置矩阵也是正交矩阵

向量之间点乘的计算公式：
向量A(Xa,Ya,Za)A (Xa,Ya,Za)，向量B(Xb,Yb,Zb)B (Xb,Yb,Zb)
A⋅B=Xa×Xb+Ya×Yb+Za×ZbA·B = Xa \times Xb + Ya \times Yb + Za \times Zb

点乘结果 = 0 两个向量夹角为直角

与向量模长和单位向量知识延伸出：如果向量和自己的点乘结果为1，则该向量为单位向量：A⋅A=x2+y2+z2=1A \cdot A = x^2+y^2+z^2=1

M=(−I−−II−−III−)，MT=(∣∣∣IIIIII∣∣∣)(这里的I,II,III不是矩阵内的元素，而是代表某一行（列），可以视为一个行（列）向量)MMT=(−I−−II−−III−)(∣∣∣IIIIII∣∣∣)=(I⋅II⋅III⋅IIIII⋅III⋅IIII⋅IIIIII⋅IIII⋅IIIII⋅III)∵M是正交矩阵∴MMT=MTM=I∴MMT=(I⋅II⋅III⋅IIIII⋅III⋅IIII⋅IIIIII⋅IIII⋅IIIII⋅III)=(100010001)∴{I⋅I=II⋅II=III⋅III=1I⋅II=II⋅I=I⋅III=III⋅I=II⋅III=III⋅II=0M = \begin{pmatrix} - & I & - \\ - & II & - \\ - & III & - \\ \end{pmatrix} ，M^T = \begin{pmatrix} | & | & | \\ I & II & III \\ | & | & | \\ \end{pmatrix}\\ (这里的I,II,III不是矩阵内的元素，而是代表某一行（列），可以视为一个行（列）向量) \\ MM^T = \begin{pmatrix} - & I & - \\ - & II & - \\ - & III & - \\ \end{pmatrix}\begin{pmatrix} | & | & | \\ I & II & III \\ | & | & | \\ \end{pmatrix} = \begin{pmatrix} I \cdot I & I \cdot II & I \cdot III \\ II \cdot I & II \cdot II & II \cdot III \\ III \cdot I & III \cdot II & III \cdot III \\ \end{pmatrix} \\ \quad \\ \because \quad M是正交矩阵 \\ \quad \therefore \quad MM^T = M^TM = I \\ \therefore \quad MM^T = \begin{pmatrix} I \cdot I & I \cdot II & I \cdot III \\ II \cdot I & II \cdot II & II \cdot III \\ III \cdot I & III \cdot II & III \cdot III \\ \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix} \\ \therefore \quad \begin{cases} I \cdot I = II \cdot II = III \cdot III = 1 \\ I \cdot II = II \cdot I = I \cdot III = III \cdot I = II \cdot III = III \cdot II = 0 \end{cases}

根据以上内容，可以得到结论：

  1. 正交矩阵的每一行，都是单位向量（自己点乘自己结果为1）
  2. 正交矩阵的每一行，都彼此互相垂直（彼此点乘结果为0）
  3. 以上结论对正交矩阵的每一列也适用，因为正交矩阵的转置也是正交矩阵

如何判断正交矩阵

根据正交矩阵的基本概念，我们可以总结出判断一个矩阵是否是正交矩阵的方式有：

  1. 判断MMT=MTM=IMM^T = M^TM = I​，满足则为正交矩阵

  2. 判断矩阵的每一行（列）是否是 单位向量
    ​nn 维向量 v=(v1,v2,...,vn)v = (v_1, v_2, ..., v_n)， 向量模长：∣v∣=v12+v22+...+vn2=1|v| = \sqrt{v_1^2 + v_2^2 + ... + v_n^2} = 1
    同时，判断矩阵的行（列）向量是否彼此正交（垂直）：v⋅u=0v \cdot u = 0

    满足则为正交矩阵

正交矩阵的重要性质

如果矩阵 MM 为正交矩阵

  1. MTM^T 也为正交矩阵
  2. MT=M−1M^T = M^{−1}
  3. 正交矩阵的行列式为 1 或 -1
  4. 正交矩阵的 各行都是单位向量且彼此正交（垂直）
  5. 正交矩阵的 各列都是单位向量且彼此正交（垂直）

列矩阵和行矩阵

  1. 列矩阵和行矩阵的基本概念

    列矩阵就是只有一列的矩阵；行矩阵就是只有一行的矩阵。他们一般用于表示向量
    把向量作为列矩阵和行矩阵与矩阵进行乘法运算时，计算顺序（列在后，行在前）和结果是不同的

  2. 列矩阵和行矩阵在Unity中的使用规则

    在Unity的Shader开发中，我们采用列矩阵的形式进行向量计算，利用结合律，我们可以从右往左阅读

    CBAv=C(B(Av))CBAv = C(B(Av))

    如果想要使用行矩阵计算出和列矩阵相同的结果，我们可以乘以变换矩阵的转置矩阵

    vATBTCT=(vAT)BT)CTvA^TB^TC^T = (vA^T)B^T)C^T

在Unity Shader开发中我们经常会对向量进行矩阵运算，
而在Unity的三维坐标系中向量一般都是三维向量（x,y,z）（x,y,z），
由于要进行矩阵计算，我们就需要把向量用矩阵表示。
通过我们之前对矩阵的学习，三维向量的矩阵表示，可以有两种：

  1. 列矩阵：只有一列的矩阵

    [xyz]\begin{bmatrix} x \\ y \\ z \\ \end{bmatrix}

  2. 行矩阵：只有一行的矩阵

    [xyz]\begin{bmatrix} x & y & z \end{bmatrix}

在进行向量的矩阵运算时，把它作为列矩阵和行矩阵得到的运算结果是不同的

假设一个矩阵：

M=[m11m12m13m21m22m23m31m32m33]M = \begin{bmatrix} m_{11} & m_{12} & m_{13} \\ m_{21} & m_{22} & m_{23} \\ m_{31} & m_{32} & m_{33} \end{bmatrix}

一个向量以列或行矩阵的形式和它进行计算时，它们的计算顺序会有不同，结果也会有不同

  1. 列矩阵：为了能和 3×33 \times 3 矩阵进行乘法运算，列矩阵必须放在右侧才能进行计算

    [m11m12m13m21m22m23m31m32m33][xyz]=[m11x+m12y+m13zm21x+m22y+m23zm31x+m32y+m33z]\begin{bmatrix} m_{11} & m_{12} & m_{13} \\ m_{21} & m_{22} & m_{23} \\ m_{31} & m_{32} & m_{33} \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ \end{bmatrix} = \begin{bmatrix} m_{11}x + m_{12}y + m_{13}z \\ m_{21}x + m_{22}y + m_{23}z \\ m_{31}x + m_{32}y + m_{33}z \end{bmatrix}

  2. 行矩阵：为了能和 3×33 \times 3 矩阵进行乘法运算，行矩阵必须放在左侧才能进行计算

    [xyz][m11m12m13m21m22m23m31m32m33]=[m11x+m21y+m31zm12x+m22y+m32zm13x+m23y+m33z]\begin{bmatrix} x & y & z \end{bmatrix}\begin{bmatrix} m_{11} & m_{12} & m_{13} \\ m_{21} & m_{22} & m_{23} \\ m_{31} & m_{32} & m_{33} \end{bmatrix} = \begin{bmatrix} m_{11}x + m_{21}y + m_{31}z & m_{12}x + m_{22}y + m_{32}z & m_{13}x + m_{23}y + m_{33}z \end{bmatrix}

注意：两种计算方式结果虽然都是3个元素组成的列矩阵和行矩阵，但是结果是不同的

列矩阵和行矩阵在Unity中的使用规则

在标准的线性代数中，矩阵和向量的乘法是按列进行的。
在 Unity 的 Shader开发中，为了和标准的数学和线性代数概念保持一致，
更加便于理解和应用，它也遵循这种矩阵乘法的定义，也就是：
将向量表示为列矩阵进行计算

[m11m12m13m21m22m23m31m32m33][xyz]=[m11x+m12y+m13zm21x+m22y+m23zm31x+m32y+m33z]\begin{bmatrix} m_{11} & m_{12} & m_{13} \\ m_{21} & m_{22} & m_{23} \\ m_{31} & m_{32} & m_{33} \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ \end{bmatrix} = \begin{bmatrix} m_{11}x + m_{12}y + m_{13}z \\ m_{21}x + m_{22}y + m_{23}z \\ m_{31}x + m_{32}y + m_{33}z \end{bmatrix}

使用列矩阵的结果是，我们的阅读顺序是从右到左的，
假设向量为列矩阵 vv，AA、BB、CC 分别为3个变换矩阵 CBAv=C(B(Av))CBAv = C(B(Av)) （矩阵乘法满足结合律）
即先对 向量 vv 使用 AA 进行变换，再依次使用 BB、CC 进行变换

注意：如果想把向量作为行矩阵处理，也是可以的，为了让行矩阵计算结果和列矩阵相同，我们可以采用以下规则

  • 列矩阵： CBAv=C(B(Av))CBAv = C(B(Av))
  • 等价于行矩阵：vATBTCT=(vAT)BT)CTvA^TB^TC^T = (vA^T)B^T)C^T

行矩阵必须乘以变换矩阵的转置矩阵才能保证计算结果和列矩阵结果一致

‍