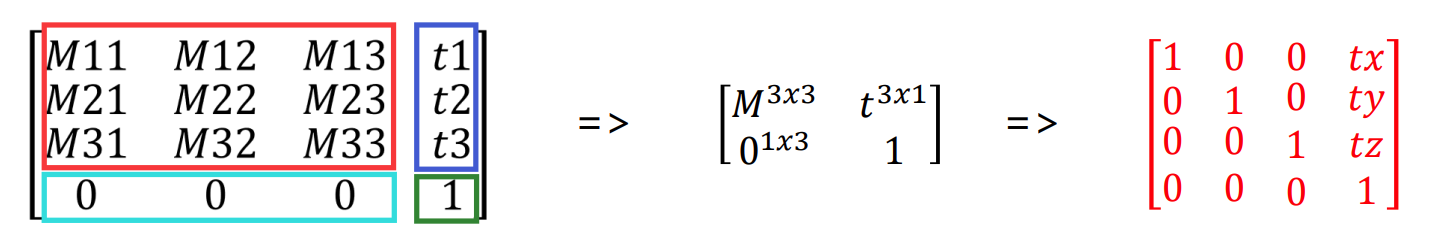US2S1L6——平移矩阵

知识回顾

  1. 三维空间中的点或向量，我们使用齐次坐标进行矩阵运算
    ​(x,y,z,w)(x , y , z , w)，其中 w=1w = 1 时 代表是一个点，w=0w = 0 时 代表一个向量
  2. 在Unity的Shader开发中
    我们采用列矩阵的形式进行向量计算，利用结合律，我们可以从右往左阅读
    CBAv=C(B(Av))CBAv = C(B(Av))

基础变换矩阵的构成规则

通过上节课齐次坐标的学习，我们知道：4×44 \times 4 的矩阵为仿射矩阵
它不仅可以表示出线性变换（缩放、旋转等），还可以表示出平移变换。

因此，我们将要学习的平移、缩放、旋转相关的变换，将会使用 4×44 \times 4 的矩阵来进行计算

4×44 \times 4 矩阵的基本构成规则为：

[M11M12M13txM21M22M23tyM31M32M23tz0001]\begin{bmatrix} M_{11} & M_{12} & M_{13} & tx \\ M_{21} & M_{22} & M_{23} & ty \\ M_{31} & M_{32} & M_{23} & tz \\ 0 & 0 & 0 & 1 \end{bmatrix}

​image​

  1. 矩阵的 M3×3M^{3 \times 3} 部分用于表示旋转和缩放变换
  2. 矩阵的 t3×1t^{3 \times 1} 部分用于表示平移
  3. 矩阵的 01×30^{1\times3} 部分始终为零矩阵
  4. 矩阵的 右下角元素 始终为 1

平移矩阵的构成

平移矩阵的构成遵循 基础变换矩阵的构成规则

[100tx010ty001tz0001]\begin{bmatrix} 1 & 0 & 0 & tx \\ 0 & 1 & 0 & ty \\ 0 & 0 & 1 & tz \\ 0 & 0 & 0 & 1 \end{bmatrix}

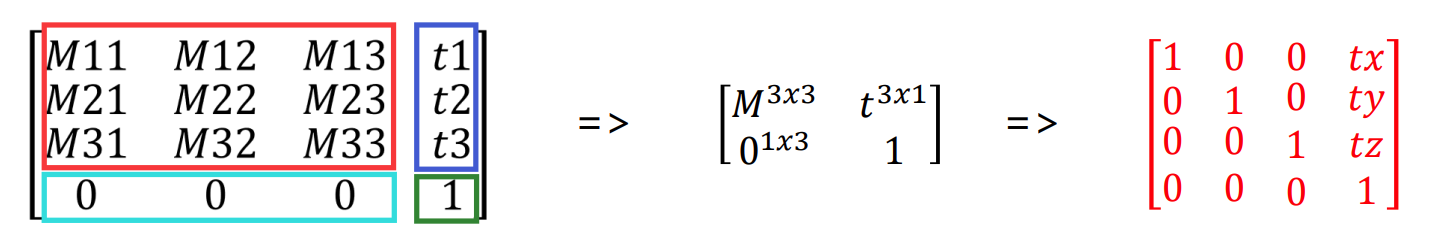
​image​

平移矩阵的构成规则为：

  1. 矩阵的 M3×3M^{3 \times 3} 部分为 3×33 \times 3 单位矩阵
  2. 矩阵的 t3×1t^{3 \times 1} 部分用于表示 x,y,zx,y,z 平移多少单位

平移矩阵的计算

与点之间的计算（使用向量的齐次坐标进行计算，ww 为 1，代表是一个点）

[100tx010ty001tz0001][xyz1]=[x+txy+tyz+tz1]\begin{bmatrix} 1 & 0 & 0 & tx \\ 0 & 1 & 0 & ty \\ 0 & 0 & 1 & tz \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = \begin{bmatrix} x + tx \\ y + ty \\ z + tz \\ 1 \end{bmatrix}

从该计算便可以看出为什么 3×33 \times 3 的矩阵无法表示平移，而需要使用齐次坐标 4×44 \times 4 的矩阵
点的 x,y,zx,y,z 分量分别增加了一个位置偏移，在几何图像中的效果就是，将点 (x,y,z)(x,y,z) 在3D空间中平移了 (tx,ty,tz)(tx,ty,tz) 个单位

与向量之间的计算（使用向量的齐次坐标进行计算，ww 为 0，代表是一个向量）

[100tx010ty001tz0001][xyz0]=[xyz0]\begin{bmatrix} 1 & 0 & 0 & tx \\ 0 & 1 & 0 & ty \\ 0 & 0 & 1 & tz \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 0 \end{bmatrix} = \begin{bmatrix} x \\ y \\ z \\ 0 \end{bmatrix}

从该计算可以发现，向量的平移结果是不会有任何变化的。
原因是因为向量其实没有位置属性，向量是由方向和大小组合的几何对象，
不管它在空间当中如何移动，它代表的方向和大小都是不会变化的，相当于在任意位置都是彼此平行的，长度不变的。
因此，对向量进行平移变换，不会改变向量。

这也是为什么需要用齐次坐标来区分 点 与 向量 ，为什么1是点，0是向量

平移矩阵是否是正交矩阵（通过转置矩阵不可得逆矩阵）

肉眼可见，平移矩阵并不是正交矩阵（参见正交矩阵中讲解的判断方式）

[100tx010ty001tz0001]\begin{bmatrix} 1 & 0 & 0 & tx \\ 0 & 1 & 0 & ty \\ 0 & 0 & 1 & tz \\ 0 & 0 & 0 & 1 \end{bmatrix}

为什么要判断它是否是正交矩阵呢？因为正交矩阵的 MT=M−1M^T = M^{−1}
如果它是正交矩阵，我们可以很快地得到它的逆矩阵，得到逆矩阵，我们就可以用于得到变换的逆向变换
（把平移过的点再通过和逆矩阵相乘将其平移回去）

因为平移矩阵不是正交矩阵，所以我们需要计算它的逆矩阵

[100tx010ty001tz0001]−1=[100−tx010−ty001−tz0001]\begin{bmatrix} 1 & 0 & 0 & tx \\ 0 & 1 & 0 & ty \\ 0 & 0 & 1 & tz \\ 0 & 0 & 0 & 1 \end{bmatrix}^{-1} = \begin{bmatrix} 1 & 0 & 0 & -tx \\ 0 & 1 & 0 & -ty \\ 0 & 0 & 1 & -tz \\ 0 & 0 & 0 & 1 \end{bmatrix}

从该逆矩阵的结构，我们便可以得知可以利用逆矩阵来计算逆向变换