US2S1L11——坐标空间的变换规则

坐标空间的组成

想要定义一个坐标空间，我们必须要具备以下两点：

1. 坐标原点位置
2. 3个坐标轴的方向（三维坐标系中）

有了这两点信息，我们就能够决定一个坐标空间了

坐标空间之间的关系

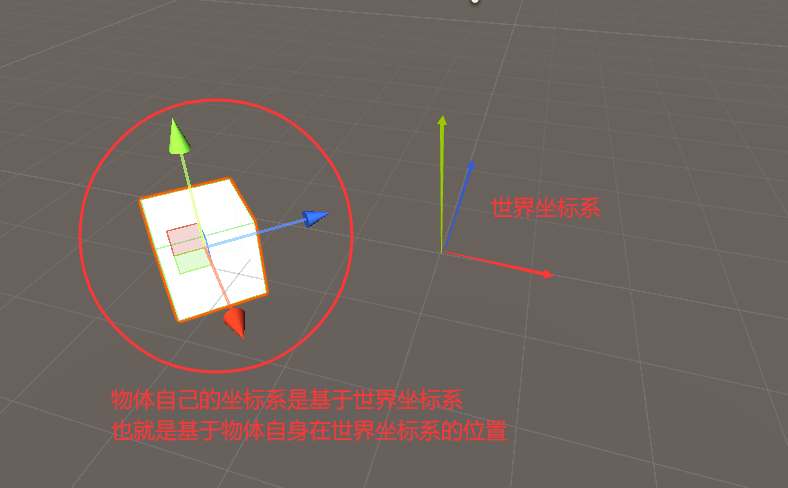
在Unity中，世界坐标空间相当于我们的基础坐标空间，Unity中其他的大部分坐标空间，都是世界坐标空间的子坐标空间。
这些子坐标空间的原点和轴向的相关表示数据，都是基于世界坐标空间的。

因此，在Unity中坐标空间之间会形成一种层级结构，大部分坐标空间都是另一个坐标空间的子空间。
所以，Unity中的坐标空间的变换实际上就是父空间和子空间之间对点或向量进行变换。

​​

坐标空间的变换矩阵

• 从子坐标空间到父坐标空间的变换矩阵：

  $$M_{s-f} = \begin{pmatrix} | & | & | & | \\ X_s & Y_s & Z_s & O_s \\ | & | & | & | \\ 0 & 0 & 0 & 1 \end{pmatrix}$$

  其中，$X_s,Y_s,Z_s$ 是子坐标系的三个轴向的方向向量（不一定是单位向量），$O_s$ 是子坐标空间的原点在父坐标空间上的坐标
  对于存在缩放的子坐标空间，需要用 $x,y,z$ 轴向的单位向量 $\times$ 对应轴的缩放因子，详见：使用坐标变换规则进行模型空间变换

  $$M_{s-f} = \begin{pmatrix} kx & 0 & 0 & 0 \\ 0 & ky & 0 & 0 \\ 0 & 0 & kz & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} | & | & | & | \\ X_s & Y_s & Z_s & O_s \\ | & | & | & | \\ 0 & 0 & 0 & 1 \end{pmatrix}$$

• 从父坐标空间到子坐标空间的变换矩阵：

  $$M_{f-s} = M_{s-f}^{-1}$$

推导坐标空间的变换矩阵

利用目前学习的平移、旋转、缩放矩阵，看起来是无法完成坐标空间之间的变换的。
我们必须对坐标空间的变换矩阵进行分析，才能得到我们想要的变换矩阵。

我们通过上一个知识点了解到，坐标空间之间是会存在父子关系的。
那么我们现在假设一个父坐标空间为 $F$ ，子坐标空间为 $S$ 。
我们已知 $S$ 坐标空间的原点位置和3个单位坐标轴（基于F坐标空间的数据表达）

对于坐标空间转换我们一般会有以下两种需求：

• 把子坐标空间 $S$ 下的点或向量 $A_s$ 转换到父坐标空间 $F$ 中为 $A_f$
• 把父坐标空间 $F$ 下的点或向量 $B_f$ 转换到子坐标空间 $S$ 中为 $B_s$

如果用矩阵来表示的话：

• $Af = M_{s-f} \cdot As$ —— $M_{s-f}$ 代表从子坐标空间到父坐标空间的变换矩阵
• $B_s = M_{f-s} \cdot B_f$ —— $M_{f-s}$ 是 $M_{s-f}$​ 的逆矩阵（我们之前学习过逆矩阵可以进行逆向变换），代表父到子的变换矩阵

也就是说我们只要知道 $M_{s-f}$ 和 $M_{f-s}$ 的其中一个矩阵，另一个矩阵都可以通过求逆矩阵得到对应的结果
那么接下来，我们就来推导 $M_{s-f}$，也就是子坐标空间到父坐标空间的变换矩阵

推导 $M_{s-f}$ ，也就是子坐标空间到父坐标空间的变换矩阵

• 已知：

  • 子坐标空间 $S$ 的原点为 $O_s$ （基于 $F$ 父坐标空间的数据表示）​
  • 子坐标空间 S 的 $x,y,z$ 轴的方向向量 $X_s,Y_s,Z_s$（基于 $F$ 父坐标空间的数据表示）

  以 Unity 的物体坐标系为例，以上信息均可以通过 Transform 提供的信息得到

  ​​

• 目的：
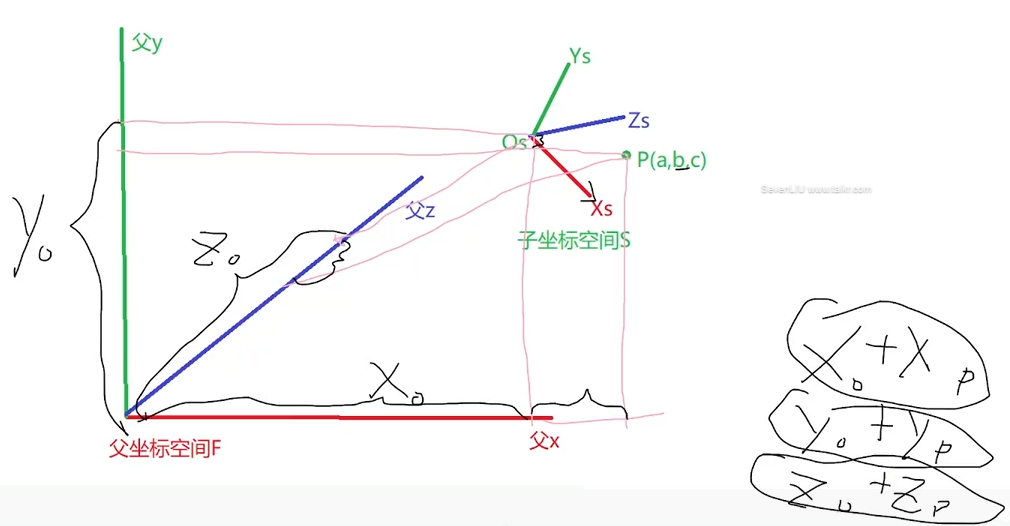
  把子坐标空间下的 点 $P(a,b,c)$ 变换到父坐标空间 $F$ 中，
  利用向量和点相关知识可以通过以下做法，达到目的：

  $$P_f = O_s + a \cdot X_s + b \cdot Y_s + c \cdot Z_s$$

  图解：

  ​

• 推导变换矩阵：

  这个向量和点相关的等式看起来和矩阵无关，但是我们可以将其变换为矩阵乘法

  $$\begin{align*} P_f & = O_s + a \cdot X_s + b \cdot Y_s + c \cdot Z_s \\ & = (X_{O_s},Y_{O_s},Z_{O_s}) + a \cdot (X_{X_s},Y_{X_s},Z_{X_s}) + b \cdot (X_{Y_s},Y_{Y_s},Z_{Y_s}) + c \cdot (X_{Z_s},Y_{Z_s},Z_{Z_s}) \\ & = (X_{O_s},Y_{O_s},Z_{O_s}) + (aX_{X_s},aY_{X_s},aZ_{X_s}) + (bX_{Y_s},bY_{Y_s},bZ_{Y_s}) + (cX_{Z_s},cY_{Z_s},cZ_{Z_s}) \\ & = (X_{O_s},Y_{O_s},Z_{O_s}) + (aX_{X_s} + bX_{Y_s} + cX_{Z_s}, \ aY_{X_s} + bY_{Y_s} + cY_{Z_s}, \ aZ_{X_s} + bZ_{Y_s} + cZ_{Z_s}) \\ & = (X_{O_s},Y_{O_s},Z_{O_s}) + \begin{pmatrix} X_{X_s} & X_{Y_s} & X_{Z_s} \\ Y_{X_s} & Y_{Y_s} & Y_{Z_s} \\ Z_{X_s} & Z_{Y_s} & Z_{Z_s} \end{pmatrix} \begin{pmatrix} a \\ b \\ c \end{pmatrix} \\ & = (X_{O_s},Y_{O_s},Z_{O_s}) + \begin{pmatrix} | & | & | \\ X_s & Y_s & Z_s \\ | & | & | \end{pmatrix} \begin{pmatrix} a \\ b \\ c \end{pmatrix} \end{align*}$$

  到此，我们已经拿到了对 $P$ 点 转换到 $P_f$ 点的 $3\times3$ 线性变换矩阵，
  我们还需要将这个线性矩阵转换为 $4\times4$ 变换矩阵，
  结合变换矩阵的构成规则，平移矩阵，齐次坐标的知识，可得到：

  $$\begin{align*} P_f & = (X_{O_s},Y_{O_s},Z_{O_s}) + \begin{pmatrix} | & | & | \\ X_s & Y_s & Z_s \\ | & | & | \end{pmatrix} \begin{pmatrix} a \\ b \\ c \end{pmatrix} = (X_{O_s},Y_{O_s},Z_{O_s},1) + \begin{pmatrix} | & | & | & 0 \\ X_s & Y_s & Z_s & 0 \\ | & | & | & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} a \\ b \\ c \\ 1 \\ \end{pmatrix} \\ & = \begin{pmatrix} 1 & 0 & 0 & X_{O_s} \\ 0 & 1 & 0 & Y_{O_s} \\ 0 & 0 & 1 & Z_{O_s} \\ 0 & 0 & 0 & 1 \end{pmatrix} + \begin{pmatrix} | & | & | & 0 \\ X_s & Y_s & Z_s & 0 \\ | & | & | & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} a \\ b \\ c \\ 1 \\ \end{pmatrix} = \begin{pmatrix} | & | & | & X_{O_s} \\ X_s & Y_s & Z_s & Y_{O_s} \\ | & | & | & Z_{O_s} \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} a \\ b \\ c \\ 1 \\ \end{pmatrix} \\ & = \begin{pmatrix} | & | & | & | \\ X_s & Y_s & Z_s & O_s \\ | & | & | & | \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} a \\ b \\ c \\ 1 \\ \end{pmatrix} \end{align*}$$

  到此，我们就拿到了 $4\times4$ 变换矩阵

• 结论：

  因此 $M_{s-f}$ 子坐标空间到父坐标空间的变换矩阵为：

  $$M_{s-f} = \begin{pmatrix} | & | & | & | \\ X_s & Y_s & Z_s & O_s \\ | & | & | & | \\ 0 & 0 & 0 & 1 \end{pmatrix}$$

  该变换矩阵的前三列分别是子坐标空间相对父坐标空间的 $x,y,z$ 轴的方向向量
  第四列是子坐标空间相对父坐标空间的原点

  由根据逆矩阵可以反向变换的性质，$M_{f-s}$ 即父坐标空间到子坐标空间的变换矩阵，
  通过 $M_{f-s} = M_{s-f}^{-1}$ 即通过子到父的变换矩阵的逆矩阵便可以得到

• 注意：

  我们在讲解时，只说了 $X_s,Y_s,Z_s$ 是轴向的方向向量，并没有说是单位方向向量
  那是因为，如果存在缩放变换的话，这3个方向向量很可能不是单位向量。

练习题

在unity中在一个模型坐标空间中有一个点P（1,0,1），该模型坐标原点为O（4,5,6）
相对世界坐标空间的x、y、z轴向的方向向量为
x：（0.71, 0, -0.71）
y：（0.5, 0.71, 0.5）
z：（0.5, -0.71, 0.5）
请利用坐标空间变换的规则，得到点P相对于世界坐标系的位置时多少？（请写出计算过程）

根据坐标空间变换矩阵的构成，由题目可得，可得到子坐标到父坐标的变换矩阵为：

$$M_{s-f} = \begin{pmatrix} 0.71 & 0.5 & 0.5 & 4 \\ 0 & 0.71 & -0.71 & 5 \\ -0.71 & 0.5 & 0.5 & 6 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix}$$

将位于模型坐标空间的点 $P(1,0,1)$ 转换为 $M_{s-f} = \begin{pmatrix} 1\\ 0 \\ 1 \\ 1 \\ \end{pmatrix}$

将点 $P$ 乘以 $M_{s-f}$，得到位于父坐标的点 $P_f$：

$$P_f = \begin{pmatrix} 0.71 & 0.5 & 0.5 & 4 \\ 0 & 0.71 & -0.71 & 5 \\ -0.71 & 0.5 & 0.5 & 6 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix} \begin{pmatrix} 1\\ 0 \\ 1 \\ 1 \\ \end{pmatrix} = \begin{pmatrix} 5.21 \\ 4.29 \\ 5.79 \\ 1 \\ \end{pmatrix}$$

‍