US2S1L12——模型空间变换

模型空间变换

  • 模型空间的意义

    模型空间的主要意义是方便我们建模，模型的顶点等数据都是基于模型空间表达的。

  • 模型空间变换指什么

    将模型空间中的点或向量通过矩阵乘法计算，变换为相对于世界坐标空间下数据

  • 如何进行模型空间变换

    • 方法一：

      认为一开始模型坐标空间和世界坐标空间重合，模型发生缩放、旋转、平移变换时
      模型空间下的点和向量也应该发生相同的变换

    • 方法二：

      用上节课学习的坐标变换规则进行计算，如果存在缩放，直接用轴向单位向量乘以对应轴缩放因子

模型空间的意义

模型空间（model space）也被称为对象空间（object space）或局部空间（local space）
它一般指3D模型的局部坐标系，每个模型都有自己独立的坐标空间，

模型空间的主要意义是方便我们建模，模型的顶点等数据都是基于模型空间表达的。

注意：在Unity中当模型移动或旋转时，模型空间坐标系也会随着变换，因为此时的模型坐标空间是世界坐标空间的子空间

模型空间中的注意事项

在模型空间中，我们一般会有 上、下、左、右、前、后 六种方向概念
Unity使用的是左手坐标系，因此模型空间的x、y、z轴，对应的是模型的右、上、前三个方向。

需要注意的是在不同的软件中，比如3DMax和Maya中模型空间中的x、y、z不见得是上面这种关系，
因此在开发时，需要让美术同学导出模型时，修改相关设置，让模型导出后能够满足Unity中的规范
详见：U3L17——模型导入相关设置

​image​

模型空间变换指什么

本课程中的模型空间变换指的主要是：
将模型空间中的点或向量通过矩阵乘法计算，变换为相对于世界坐标空间下数据

渲染管线是将数据分阶段的变为屏幕图像的过程
其中在几何阶段以及光栅化阶段中，我们需要将顶点等数据进行相关的变换，让其最终的数据能够显示在屏幕上。
而模型空间变换就是其中一个重要的变换步骤，就是将模型空间下的点和向量数据转换到世界空间下进行表示

如何进行模型空间变换

我们可以假设该机器人模型的手掌红点位置处于模型坐标空间下的（0.63, 0.84, -0.04）点
当模型在Unity中没有任何父对象，那么该模型空间的坐标系就是相对世界坐标空间的

当模型位于世界坐标原点时，当前的红点位置相对世界空间也会是（0.63, 0.84, -0.04）

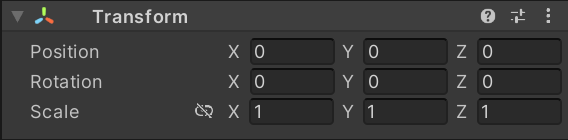
​image​

但是当模型进行缩放、旋转、平移时，该点相对世界空间就会变化。
如果我们将模型进行2倍缩放，又进行（0, 45, 0）的旋转，然后再进行(5, 0, 5)的平移，
红点的相对世界空间坐标是多少呢？

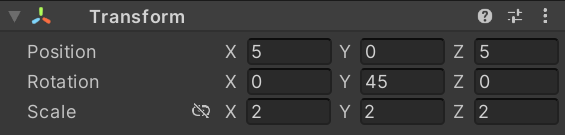
​image​

​image​

根据我们之前学习的复合运算相关的知识
在进行复合运算时，一定遵守先缩放、后旋转、再平移的规则。
我们可以得到等式如下：

P相对于世界坐标系的位置=M平移M旋转M缩放P红点的列矩阵P_{相对于世界坐标系的位置} = M_{平移}M_{旋转}M_{缩放}P_{红点的列矩阵}

因此可以计算（0.63, 0.84, -0.04）相对于世界空间的坐标：

P相对于世界坐标系的位置=M平移M旋转M缩放P红点的列矩阵=[1005010000150001][cos45∘0sin45∘00100−sin45∘0cos45∘00001][2000020000200001][0.630.84−0.041]=[5.8341.684.0521]\begin{align*} P_{相对于世界坐标系的位置} & = M_{平移}M_{旋转}M_{缩放}P_{红点的列矩阵} \\ & = \begin{bmatrix} 1 & 0 & 0 & 5 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 5 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} cos45^\circ & 0 & sin45^\circ & 0 \\ 0 & 1 & 0 & 0 \\ -sin45^\circ & 0 & cos45^\circ & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} 2 & 0 & 0 & 0 \\ 0 & 2 & 0 & 0 \\ 0 & 0 & 2 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} 0.63 \\ 0.84 \\ -0.04 \\ 1 \end{bmatrix} \\ & = \begin{bmatrix} 5.834 \\ 1.68 \\ 4.052 \\ 1 \end{bmatrix} \end{align*}

根据刚才的例子讲解，我们知道了模型空间变换的变化规则就是：

P模型空间下的点或向量相对于世界空间下的数据表达=M平移M旋转M缩放P模型空间下的点或向量P_{模型空间下的点或向量相对于世界空间下的数据表达} = M_{平移}M_{旋转}M_{缩放}P_{模型空间下的点或向量}

其中平移、旋转、缩放矩阵中的具体变换值都是相对于世界空间下的数据

原理：认为一开始模型坐标空间和世界坐标空间重合，模型发生缩放、旋转、平移变换时，模型空间下的点和向量也应该发生相同的变换

问题：

  • 当存在多层模型父子关系时

    直接一层层往上计算接口，或者直接使用 transform 当中的 position、rotation、lossyScale 属性进行计算

  • 为什么没有使用上节课讲解的坐标空间变换规则

    因为上节课的坐标变换规则是未讲解缩放相关内容

使用坐标变换规则进行模型空间变换

如果要使用坐标变换规则的矩阵进行模型空间变换，对于存在缩放的模型空间
只需要用 x,y,zx,y,z 轴向的单位向量 ×\times 对应轴的缩放因子 即可，相当于：

Ms−f=(kx0000ky0000kz00001)(∣∣∣∣XsYsZsOs∣∣∣∣0001)M_{s-f} = \begin{pmatrix} kx & 0 & 0 & 0 \\ 0 & ky & 0 & 0 \\ 0 & 0 & kz & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} | & | & | & | \\ X_s & Y_s & Z_s & O_s \\ | & | & | & | \\ 0 & 0 & 0 & 1 \end{pmatrix}

因此，根据上例计算：

P相对于世界坐标系的位置=Ms−fP红点的列矩阵=[2000020000200001][0.7100.7100100−0.7100.7100001][0.630.84−0.041]=[1.41401.41400200−1.41401.41400001][0.630.84−0.041]=[5.8341.684.0521]\begin{align*} P_{相对于世界坐标系的位置} & = M_{s-f}P_{红点的列矩阵} \\ & = \begin{bmatrix} 2 & 0 & 0 & 0 \\ 0 & 2 & 0 & 0 \\ 0 & 0 & 2 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 0.71 & 0 & 0.71 & 0 \\ 0 & 1 & 0 & 0 \\ -0.71 & 0 & 0.71 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} 0.63 \\ 0.84 \\ -0.04 \\ 1 \end{bmatrix} \\ & = \begin{bmatrix} 1.414 & 0 & 1.414 & 0 \\ 0 & 2 & 0 & 0 \\ -1.414 & 0 & 1.414 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} 0.63 \\ 0.84 \\ -0.04 \\ 1 \end{bmatrix} \\ & = \begin{bmatrix} 5.834 \\ 1.68 \\ 4.052 \\ 1 \end{bmatrix} \end{align*}

假设Unity中有一个模型空间（父空间为世界坐标空间）中的顶点P，坐标为（2,4,0）
现在将该模型平移（2,3,4）个单位，又绕Y轴旋转150度，再缩放3倍
现在请将P点进行模型空间转换得到它相对于世界坐标空间的位置：

P相对于世界坐标系的位置=M平移M旋转M缩放P红点的列矩阵=[1002010300140001][cos150∘0sin150∘00100−sin150∘0cos150∘00001][3000030000300001][2401]=[−3.1961511]\begin{align*} P_{相对于世界坐标系的位置} & = M_{平移}M_{旋转}M_{缩放}P_{红点的列矩阵} \\ & = \begin{bmatrix} 1 & 0 & 0 & 2 \\ 0 & 1 & 0 & 3 \\ 0 & 0 & 1 & 4 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} cos150^\circ & 0 & sin150^\circ & 0 \\ 0 & 1 & 0 & 0 \\ -sin150^\circ & 0 & cos150^\circ & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} 3 & 0 & 0 & 0 \\ 0 & 3 & 0 & 0 \\ 0 & 0 & 3 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} 2 \\ 4 \\ 0 \\ 1 \end{bmatrix} \\ & = \begin{bmatrix} -3.196 \\ 15 \\ 1 \\ 1 \end{bmatrix} \end{align*}

‍