US2S1L13——观察空间变换

知识回顾

  1. 在渲染管线中，顶点、法线等相关模型数据会经过以下的空间变换

    模型空间 → 世界空间 → 观察空间 → 裁剪空间 → 屏幕空间

  2. 上节课学习的模型空间变换主要指的就是

    模型空间 → 世界空间 的变换，我们称之为 模型空间变换

  3. 坐标空间变换规则一般有两种

    • 方式一：通用的坐标空间变换规则（存在缩放时，轴向单位向量*缩放因子）
    • 方式二：认为一开始模型坐标空间和世界坐标空间重合，模型发生缩放、旋转、平移变换时，模型空间下的点和向量也应该发生相同的变换

观察空间的意义

观察空间就是摄像机的模型空间，它决定了渲染的视角和视野

观察空间（view space） 也被成为 摄像机空间（camera space）
观察空间可以认为是一个特殊的模型空间，这里的模型指的是场景中的摄像机，
摄像机可以认为是一个非常特殊的模型，它不可见，但是它可以决定我们在屏幕上看到的内容，
因此我们将摄像机的模型空间单独提出来讨论和学习，并将它称为观察空间。

观察空间的主要意义是摄像机决定了渲染的视角和视野

​image​

注：这里的图标和线是Scene窗口的标记，实际游戏不可见

观察空间中的注意事项

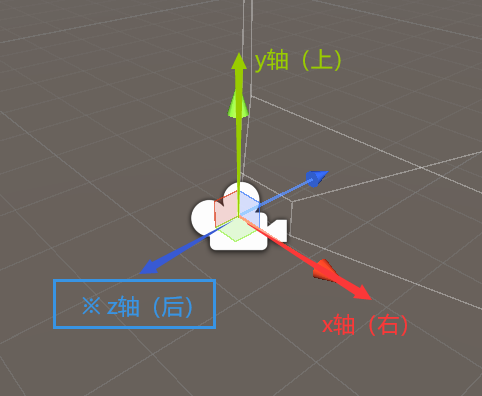
在模型空间中，我们讲过模型空间的 x,y,zx,y,z 轴，对应的是模型的右、上、前三个方向。
是因为Unity中的模型空间遵循左手坐标系原则。

但是在Unity的观察空间中，观察空间是遵循右手坐标系原则的，因此它的坐标轴方向有所不同。
观察空间中的 x,y,zx,y,z 轴的正方向，分别对应摄像机的 右、上、后方。

主要原因：
在计算机图形学的OpenGL中，为了统一处理场景中物体的渲染和投影
通常使用右手坐标系，为了方便之后的数据处理，因此在Unity当中的观察空间，也遵循右手坐标系

​image​

观察空间变换指什么

本课程中的观察空间变换指的主要是将模型空间中的点或向量从世界空间中变换到观察空间中。
它是顶点变换的第二步，就是将 数据 从 世界空间 —> 观察空间 进行变换观察空间变换也可以称为观察变换（view transform）

如何进行观察空间变换

在进行观察空间变换之前，我们首先应该利用上节课学习的知识，
将模型空间下的顶点数据变换到世界空间下
也就是需要先进行模型空间变换，我们同样利用上节课的例子，
模型空间下的顶点坐标为（0.63, 0.84, -0.04）
当模型进行2倍缩放，又进行（0,45,0）的旋转，然后再进行（5,0,5）的平移后
该顶点的世界空间下的坐标（数据表达）为（5.834, 1.68, 4.052）

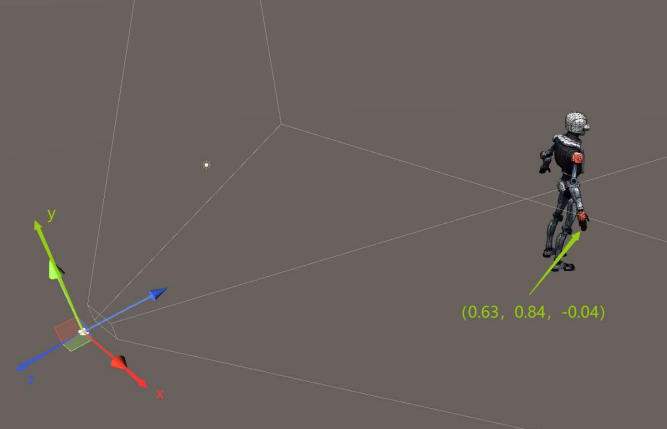
​image​

我们现在知道了该顶点的世界空间下的坐标为（5.834, 1.68, 4.052）

那么要将其变换到观察空间下有两种方式：

  1. 坐标空间变换规则

    Ms−f=(∣∣∣∣XsYsZsOs∣∣∣∣0001) Mf−s=Ms−f−1M_{s-f} = \begin{pmatrix} | & | & | & | \\ X_s & Y_s & Z_s & O_s \\ | & | & | & | \\ 0 & 0 & 0 & 1 \end{pmatrix} \\ \ \\ M_{f-s} = M_{s-f}^{-1}

    ‍

    通过如下API获取观察空间（摄像机）的方向向量以及坐标原点相对于世界坐标系的位置的信息：

    1
    2
    3
    4
    print(this.transform.right);        //x轴
    print(this.transform.up);            //y轴
    print(-this.transform.forward);        //z轴，注意，观察空间是右手坐标系，因此取后方
    print(this.transform.position);        //原点位置

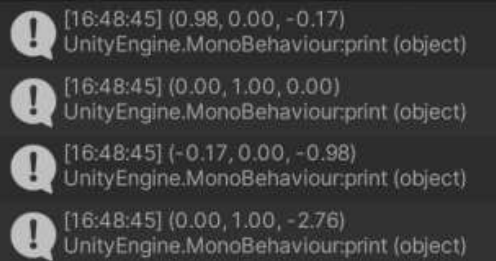
    ​image​

    因此得到观察空间到世界空间的（子到父）的变换矩阵，再对该矩阵进行逆矩阵计算，得到世界空间到观察空间（父到子）的变换矩阵

    Mf−s=Ms−f−1=(0.980−0.1700101−0.170−0.98−2.760001)−1=(0.990−0.1718−0.474010−1−0.17180−0.99−2.7330001)M_{f-s} = M_{s-f}^{-1} = \begin{pmatrix} 0.98 & 0 & -0.17 & 0 \\ 0 & 1 & 0 & 1 \\ -0.17 & 0 & -0.98 & -2.76 \\ 0 & 0 & 0 & 1 \end{pmatrix}^{-1} = \begin{pmatrix} 0.99 & 0 & -0.1718 & -0.474 \\ 0 & 1 & 0 & -1 \\ -0.1718 & 0 & -0.99 & -2.733 \\ 0 & 0 & 0 & 1 \end{pmatrix}

    用父到子的变换矩阵和目标点进行矩阵运算

    (0.990−0.1718−0.474010−1−0.17180−0.99−2.7330001)(5.8341.684.0521)=(4.5620.679−7.7221)\begin{pmatrix} 0.99 & 0 & -0.1718 & -0.474 \\ 0 & 1 & 0 & -1 \\ -0.1718 & 0 & -0.99 & -2.733 \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 5.834 \\ 1.68 \\ 4.052 \\ 1 \end{pmatrix} = \begin{pmatrix} 4.562 \\ 0.679 \\ -7.722 \\ 1 \end{pmatrix}

  2. 逆向变换观察空间

    根据摄像机的Transform提供的位置，旋转，缩放信息，对摄像机进行逆向变换，让观察空间和世界坐标空间重合，
    重合时观察空间下的点或向量的数据表达和世界空间下的数据表达式相同的

    1. 观察摄像机的Transform组件

      ​image​

    2. 根据第一步信息，获取摄像机逆向变换的矩阵，让其和世界坐标系重合

      （注意！原本是先缩放、再旋转、最后位移，因此逆向变换使需要先位移、再旋转、最后缩放）

      [cos(−10∘)0sin(−10∘)00100−sin(−10∘)0cos(−10∘)00001][1000010−10012.760001]=[0.980−0.17−0.46010−10.1700.982.70001]\begin{bmatrix} cos(-10^{\circ}) & 0 & sin(-10^{\circ}) & 0 \\ 0 & 1 & 0 & 0 \\ -sin(-10^{\circ}) & 0 & cos(-10^{\circ}) & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & -1 \\ 0 & 0 & 1 & 2.76 \\ 0 & 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} 0.98 & 0 & -0.17 & -0.46 \\ 0 & 1 & 0 & -1 \\ 0.17 & 0 & 0.98 & 2.7 \\ 0 & 0 & 0 & 1 \end{bmatrix}

    3. 由于观察空间，z轴正方向是摄像机的后方，所以我们需要对**z分量进行取反操作**

      [1000010000−100001][0.980−0.17−0.46010−10.1700.982.70001]=[0.980−0.17−0.46010−1−0.170−0.98−2.70001]\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 0.98 & 0 & -0.17 & -0.46 \\ 0 & 1 & 0 & -1 \\ 0.17 & 0 & 0.98 & 2.7 \\ 0 & 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} 0.98 & 0 & -0.17 & -0.46 \\ 0 & 1 & 0 & -1 \\ -0.17 & 0 & -0.98 & -2.7 \\ 0 & 0 & 0 & 1 \end{bmatrix}

    4. 用该变换矩阵和点进行乘法运算得到最终结果

      [0.980−0.17−0.46010−1−0.170−0.98−2.70001][5.8341.684.0521]=[4.5620.679−7.7221]\begin{bmatrix} 0.98 & 0 & -0.17 & -0.46 \\ 0 & 1 & 0 & -1 \\ -0.17 & 0 & -0.98 & -2.7 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 5.834 \\ 1.68 \\ 4.052 \\ 1 \end{bmatrix} = \begin{bmatrix} 4.562 \\ 0.679 \\ -7.722 \\ 1 \end{bmatrix}

假设Unity中有一个模型空间（父空间为世界坐标空间）中的顶点P，坐标为（2,4,0）
现在将该模型平移（2,3,4）个单位，又绕Y轴旋转150度，再缩放3倍。
场景上有一个摄像机，它所处的相对世界坐标系位置为（0,0,0）位置，旋转角度为（30,45,0）
现在请将P点进行观察空间转换得到它相对于观察空间的位置。

先求世界空间到观察空间的变换矩阵：

  1. 先对摄像机进行逆向变换，使其于世界坐标系重合，逆向旋转变换顺序：y - x - z

    [10000cos⁡30∘−sin⁡30∘00sin⁡30∘cos⁡30∘00001][cos⁡45∘0sin⁡45∘00100−sin⁡45∘0cos⁡45∘00001]=[0.707100.707100.35350.866−0.35350−0.6120.50.612300001]\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos30^{\circ} & -\sin30^{\circ} & 0 \\ 0 & \sin30^{\circ} & \cos30^{\circ} & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} \cos45^{\circ} & 0 & \sin45^{\circ} & 0 \\ 0 & 1 & 0 & 0 \\ -\sin45^{\circ} & 0 & \cos45^{\circ} & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} = \begin{bmatrix} 0.7071 & 0 & 0.7071 & 0 \\ 0.3535 & 0.866 & -0.3535 & 0 \\ -0.612 & 0.5 & 0.6123 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}

    对 z 分量取反，矩阵改变为：

    [0.707100.707100.35350.866−0.353500.6123−0.5−0.612300001]\begin{bmatrix} 0.7071 & 0 & 0.7071 & 0 \\ 0.3535 & 0.866 & -0.3535 & 0 \\ 0.6123 & -0.5 & -0.6123 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}

  2. 求转换到世界空间下的顶点：

    P相对于世界坐标系的位置=M平移M旋转M缩放P红点的列矩阵=[1002010300140001][cos150∘0sin150∘00100−sin150∘0cos150∘00001][3000030000300001][2401]=[−3.1961511]\begin{align*} P_{相对于世界坐标系的位置} & = M_{平移}M_{旋转}M_{缩放}P_{红点的列矩阵} \\ & = \begin{bmatrix} 1 & 0 & 0 & 2 \\ 0 & 1 & 0 & 3 \\ 0 & 0 & 1 & 4 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} cos150^\circ & 0 & sin150^\circ & 0 \\ 0 & 1 & 0 & 0 \\ -sin150^\circ & 0 & cos150^\circ & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} 3 & 0 & 0 & 0 \\ 0 & 3 & 0 & 0 \\ 0 & 0 & 3 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} 2 \\ 4 \\ 0 \\ 1 \end{bmatrix} \\ & = \begin{bmatrix} -3.196 \\ 15 \\ 1 \\ 1 \end{bmatrix} \end{align*}

  3. 将世界空间下的顶点转换到观察坐标下：

    [0.707100.707100.35350.866−0.353500.6123−0.5−0.612300001][−3.1961511]=[−1.55211.506−10.0691]\begin{bmatrix} 0.7071 & 0 & 0.7071 & 0 \\ 0.3535 & 0.866 & -0.3535 & 0 \\ 0.6123 & -0.5 & -0.6123 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} -3.196 \\ 15 \\ 1 \\ 1 \end{bmatrix} = \begin{bmatrix} -1.552 \\ 11.506 \\ -10.069 \\ 1 \end{bmatrix}

‍