US2S1L14——齐次裁剪空间
US2S1L14——齐次裁剪空间
视锥体
在渲染管线中,顶点、法线等相关模型数据会经过以下的空间变换(详见:US2S1L10——坐标空间的变换)
模型空间 → 世界空间 → 观察空间 → 裁剪空间 → 屏幕空间
通过之前的学习,我们已经可以将相关数据在 模型空间 → 世界空间 → 观察空间 之间进行变换
我们知道观察空间也被称为摄像机空间,此时获取到的顶点等数据都是基于摄像机空间中的数据表达,
而摄像机中有一个非常重要的概念,就是视锥体。
摄像机的视锥体是在三维空间中表示摄像机可见区域的虚拟体积,它类似一个六面体的形状,根据摄像机的属性和投影方式而定。
视锥体定义了摄像机在场景中能够看到的物体区域,超出这个区域的物体将在渲染时被裁减掉,从而提高渲染性能。
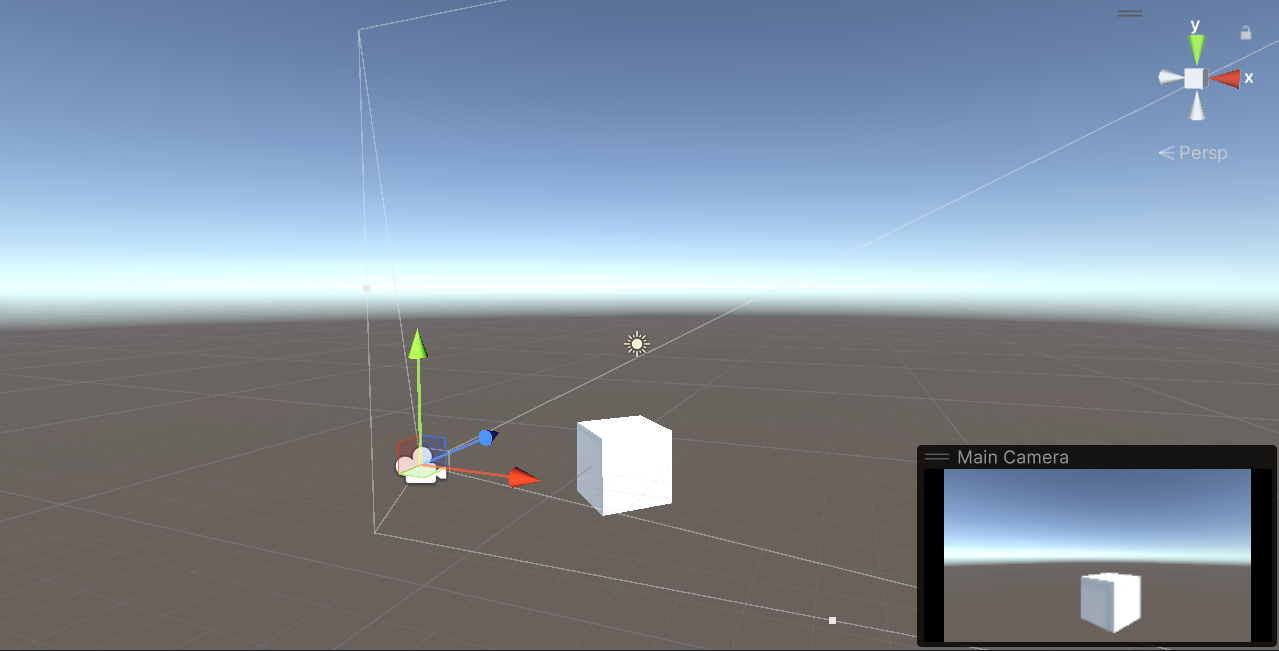
透视投影摄像机(视锥体形似金字塔,一般3D游戏使用)
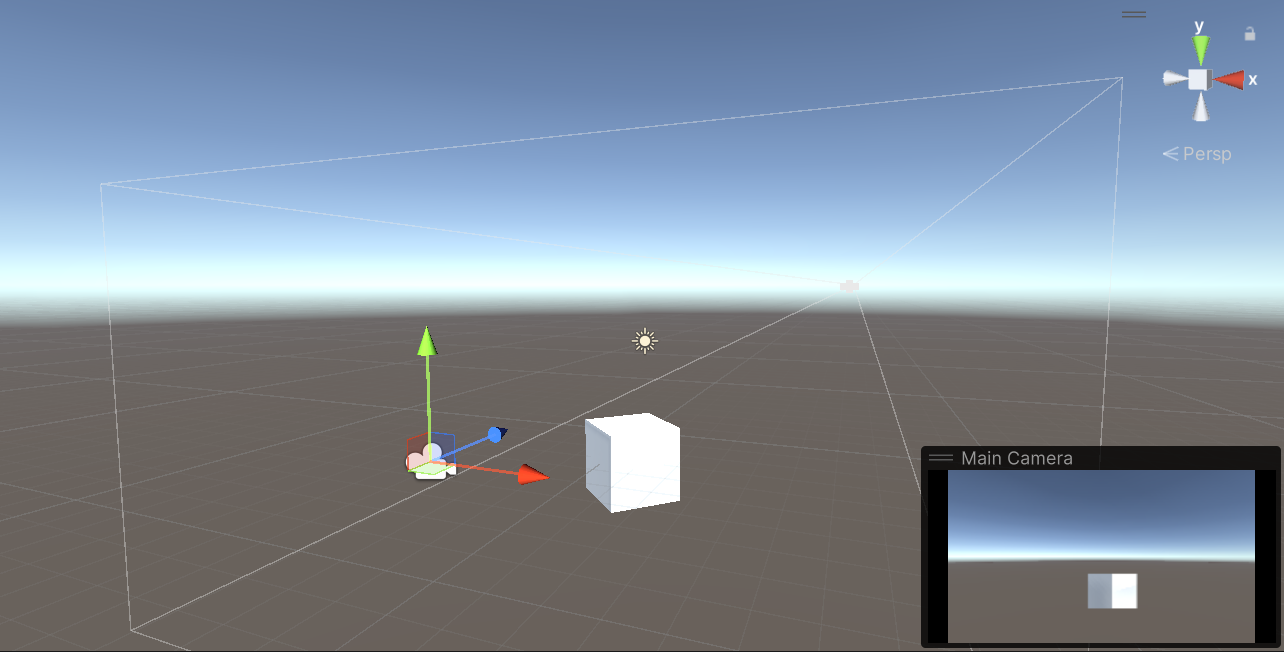
透视投影摄像机(视锥体形似立方体,一般横板2D游戏使用)
视锥体主要包含几种重要部分:
-
远近裁剪平面
-
左、右、上、下裁剪平面
-
透视投影中,视锥体类似一个金字塔形状,远裁剪面比近裁剪面大,所以产生透视效果,也就是近大远小

-
正交投影中,视锥体类似于长方体的形状,远近裁剪平面大小一致,不会产生透视效果,即无论多远都一样大

之前提到,我们希望根据视锥体围成的区域对顶点等数据进行裁剪,
超出视锥体这个范围的坐标在渲染时会被裁减掉,只保留视锥体范围内的坐标。
但是,如果直接使用视锥体定义的空间来进行裁剪,那不同的视锥体就需要不同的处理过程,
而且对于透视投影的视锥体来说,判断顶点是否在范围内相对较麻烦。
因此,我们希望用更通用、便捷的方式来进行裁剪工作,就需要将观察空间(摄像机空间)中的数据转换到**齐次裁剪空间**中
齐次裁剪空间
裁剪空间 也被称为 齐次裁剪空间。 齐次裁剪空间(裁剪空间)是一个非常特殊的坐标空间
注意,Unity的齐次裁剪空间是左手坐标系,因此从观察空间转换为齐次裁剪空间矩阵时,必须要对z分量取反
很多同学可能都是第一次听到这个名词,在以前的数学学科当中可能都没有学习过。
齐次裁剪空间 是一个三维空间,是在计算机图形学中用于在图形渲染过程中进行裁剪和投影的。
它的坐标范围为(-1,-1,-1)到(1,1,1),超出这个范围的坐标在渲染时会被裁减掉,只会保留范围内的坐标。
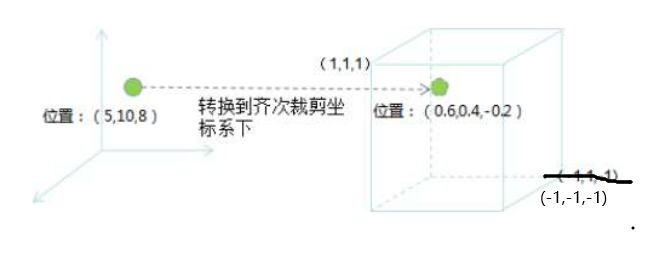
我们之后的几节课主要要学习的就是视锥体的 透视投影 和 正交投影 对应的裁剪矩阵(投影矩阵)
通过裁剪矩阵我们就可以将观察空间中的数据转换到齐次裁剪空间中了。
目前只要知道。齐次裁剪空间是通过将摄像机的视锥体投影到一个规范化的立方体而转换来的。这个立方体就是齐次裁剪空间。
