US2S1L17——透视投影变换

透视投影变换

• 获取透视投影的摄像机重要参数

  • Near：近裁剪面离摄像机的距离

  • Far：远裁剪面离摄像机的距离

  • FOV（Field of View）：决定视锥开口角度

  • Aspect：屏幕宽高比

  • 近裁剪面

    • $近裁剪面高 = 2 \times Near \times \tan(\frac{FOV}{2})$
    • $近裁剪面宽 = Aspect \times 近裁剪面高 = Aspect \times 2 \times Near \times \tan(\frac{FOV}{2})$

  • 远裁剪面

    • $远裁剪面高 = 2 \times Far \times \tan(\frac{FOV}{2})$
    • $远裁剪面宽 = Aspect \times 远裁剪面高 = Aspect \times 2 \times Far \times \tan(\frac{FOV}{2})$

• 透视投影变换到裁剪空间的矩阵

  1. 近裁剪面上的所有点保持不变
  2. 远裁剪面的z值不变，远裁剪面的中心点不变
  3. 远裁剪面宽高映射成近裁剪面的宽高

  得到了最终的变换矩阵：

  $$\begin{pmatrix} \frac{1}{Aspect \cdot \tan(\frac{FOV}{2})} & 0 & 0 & 0 \\ 0 & \frac{1}{\tan(\frac{FOV}{2})} & 0 & 0 \\ 0 & 0 & -\frac{Far + Near}{Far - Near} & -\frac{2 Far\cdot Near}{Far - Near} \\ 0 & 0 & -1 & 0 \\ \end{pmatrix}$$

  注意，由该矩阵转换出来的四维齐次坐标$(x',y',z',w')$，其 $w'$ 很有可能不是1，
  这时我们可以对坐标除以 $w'$ 标量，使其为1，这样得到的 $\frac{x'}{w},\frac{y'}{w},\frac{z'}{w}$，如果在 $(-1,1)$ 内就是不需要裁剪的
  或者我们可以直接判断 $x',y',z'$ 是否在 $(-w',w')$ 内，如果是就不需要裁剪

明确透视投影变换目标

我们这节课的目标就是要得到 将摄像机视锥体的 透视投影 转换到 齐次坐标系 时的 变换矩阵

我们可以将其分成三步来完成：

1. 将透视视锥体变成一个长方体，将该长方体进行正交投影变换的操作（远裁剪面向z轴压缩，xy缩小而z不变）
2. 将视锥体中心位移到观察空间原点中心
3. 将长方体视锥体的$x,y,z$坐标范围映射到(-1,1)长宽高为2的正方体中

​​

Unity中透视投影重要参数

Camera详细参数可见：U1L10-1——Camera可编辑参数相关，透视投影相关具体参数：Projection，Clipping Planes

​​

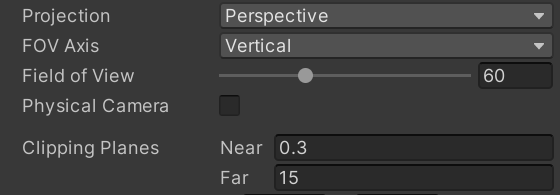
• Projection - 摄像机投影模式

  • Perspective 透视模式（不考虑Physical Camera参数）

    • Field of view - FOV，决定视锥开口角度

  • orthographic 正交摄像机（一般用于2D游戏制作）

• Clipping Planes - 裁剪平面距离

  • Near：近裁剪面离摄像机的距离
  • Far：远裁剪面离摄像机的距离

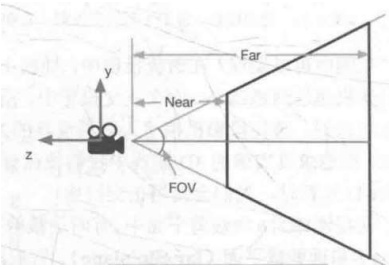
根据已知参数，获取到远近裁剪面的高度：

• 已知：

  • Near：近裁剪面离摄像机的距离
  • Far：远裁剪面离摄像机的距离
  • Field of view - FOV，决定视锥开口角度

• 可得：

  • $近裁剪面高 = 2 \times Near \times \tan(\frac{FOV}{2})$
  • $远裁剪面高 = 2 \times Far \times \tan(\frac{FOV}{2})$

​​

现在我们已经可以得到远近裁剪面高，我们还需要知道远近裁剪面的宽，以便之后进行变换矩阵的推导
可以通过摄像机参数Camera.aspect​得到Game窗口的宽高比

Aspect = 宽 : 高 = 宽 / 高

因此可得远近裁剪面宽：

• $近裁剪面宽 = Aspect \times 近裁剪面高 = Aspect \times 2 \times Near \times \tan(\frac{FOV}{2})$
• $远裁剪面宽 = Aspect \times 远裁剪面高 = Aspect \times 2 \times Far \times \tan(\frac{FOV}{2})$

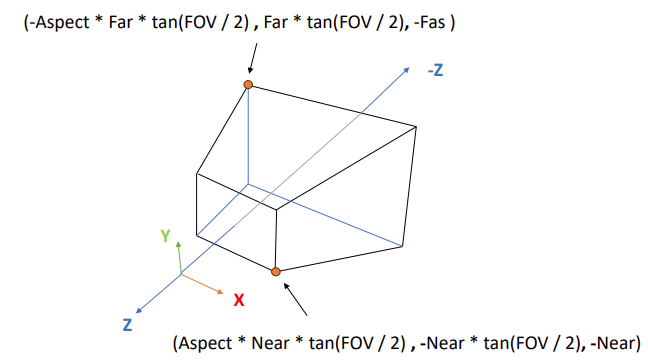
于是，现在我们就可以得到在观察空间下，视锥体各个点的坐标：

​​

透视投影变换矩阵的推导

1. 将透视视锥体变成一个长方体，将该长方体进行正交投影变换的操作

   想要实现右图的变换，我们需要满足3个特性：

   1. 近裁剪面上的所有点保持不变
   2. 远裁剪面的z值不变，远裁剪面的中心点不变
   3. 远裁剪面宽高映射成近裁剪面的宽高

   ​​

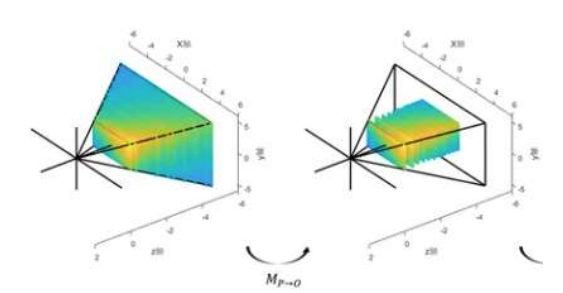
   我们只需要根据这3个特性得到对应的矩阵变换关系，然后进行推导即可

   假设将透视视锥体变换为长方体视锥体的矩阵为 $M_{变化矩阵}$​

   1. 近裁剪面上的所有点保持不变

      近裁剪面上的点 $(x,y,Near,1)$ 变换后还是 $(x,y,Near,1)$​

      $$M_{变化矩阵} \begin{pmatrix} x \\ y \\ -Near \\ 1 \end{pmatrix} = \begin{pmatrix} x \\ y \\ -Near \\ 1 \end{pmatrix}(注意，这里的Near是基于观察空间的，故为负数)$$

      其中，$x$ 和 $y$ 等于0时，相当于就是近裁剪面的中心点，也满足下面的等式：

      $$M_{变化矩阵} \begin{pmatrix} 0 \\ 0 \\ -Near \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ -Near \\ 1 \end{pmatrix}$$

   2. 远裁剪面的z值不变，远裁剪面的中心点不变

      相当于 $z$ 轴与远裁剪面的交点 $(0,0,Far,1)$ 变换后仍为 $(0,0,Far,1)$

      $$M_{变化矩阵} \begin{pmatrix} 0 \\ 0 \\ -Far \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ -Far \\ 1 \end{pmatrix}(注意，这里的Far是基于观察空间的，故为负数)$$

   3. 远裁剪面宽高映射成近裁剪面的宽高

      这一步相对来说复杂一些，我们需要利用之前学习的知识点来进行一些推导：

      1. 透视投影视锥体内**顶点和原点连接，在近裁剪面的交点为投影点**

         ​​

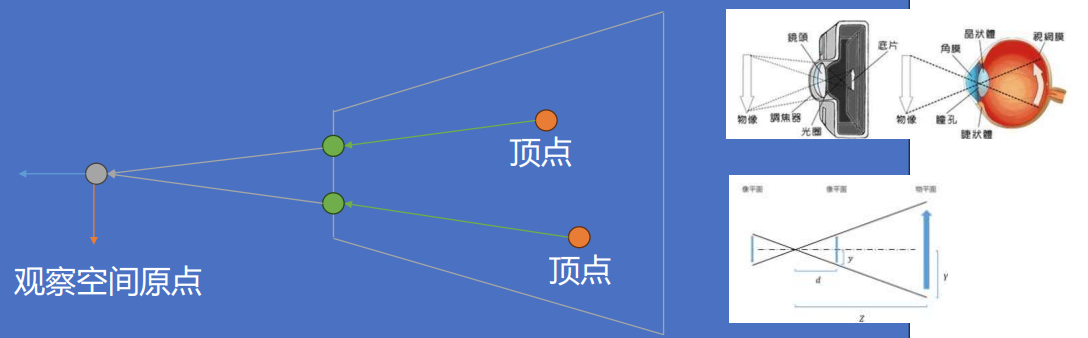
      2. 相似三角形的对应边成比例（$k$ 称为相似比）

         $$\frac{a}{a'} = \frac{b}{b'} = \frac{c}{c'} = k$$

         ​​

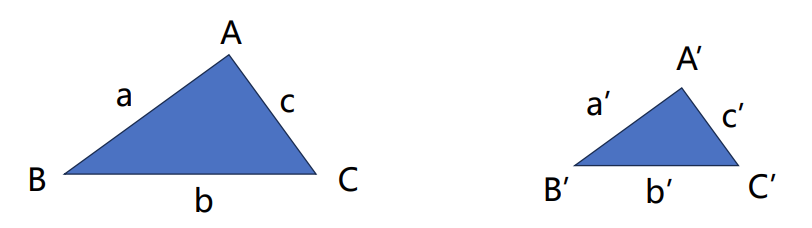
      根据上面的知识，结合下图，可以推导出：

      假设一个视锥体内的点坐标为 $(X,Y,Z)$，经过透视视锥体变换为长方体视锥体以后坐标变为 $(X',Y',Z)$：

      • $x$ 轴变换情况：

        $$\frac{X'}{X} = \frac{-Near}{Z} \Rightarrow X' = X \cdot \frac{-Near}{Z}$$

      • $y$ 轴变换情况：

        $$\frac{Y'}{Y} = \frac{-Near}{Z} \Rightarrow Y' = Y \cdot \frac{-Near}{Z}$$

      • 已知 $z$ 轴不变

      ​​

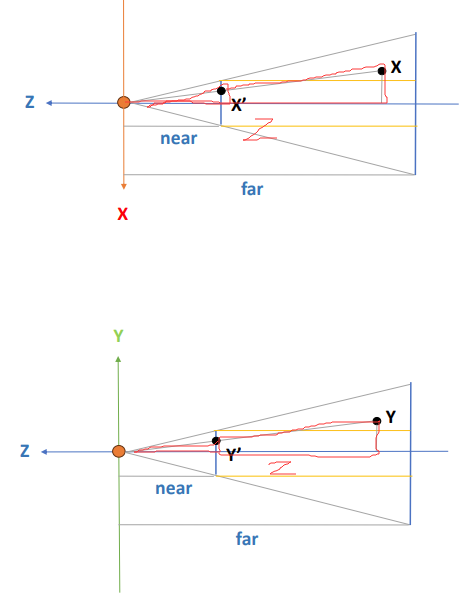
      通过此推导可得，视锥体内的所有点的$x,y$坐标都经过了同样的缩放，缩放因子为：$\frac{-near}{Z}$

      因此可以推导：

      $$M_{变化矩阵} \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} x\frac{-Near}{Z} \\ y\frac{-Near}{Z} \\ 未知 \\ 1 \end{pmatrix}$$

   通过三小步的推导，我们得到三个与 $M_{变化矩阵}$ 相关的等式：

   $$\begin{cases} M_{变化矩阵} \begin{pmatrix} 0 \\ 0 \\ -Near \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ -Near \\ 1 \end{pmatrix} \\ \ \\ M_{变化矩阵} \begin{pmatrix} 0 \\ 0 \\ -Far \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ -Far \\ 1 \end{pmatrix} \\ \ \\ M_{变化矩阵} \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} x\frac{-Near}{Z} \\ y\frac{-Near}{Z} \\ 未知 \\ 1 \end{pmatrix} \end{cases}$$

   根据上面三个等式，推导 $M_{变化矩阵}$，步骤如下：

   补充知识点： 四维齐次坐标乘以非零标量后，它映射的三维空间中的点不变 。我们通过该知识点对等式进行变形

   1. 先从信息最多的第三个等式来进行推导

      首先对最终的结果进行一次变形

      $$\because \begin{pmatrix} x\frac{-Near}{Z} \\ y\frac{-Near}{Z} \\ 未知 \\ 1 \end{pmatrix} \times -z = \begin{pmatrix} x \cdot Near \\ y \cdot Near \\ 未知 \\ -z \end{pmatrix} (映射的点不变) \\ \ \\ \therefore M_{变化矩阵} \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} x \cdot Near \\ y \cdot Near \\ 未知 \\ -z \end{pmatrix}$$

      根据上式得到的结果，对 $M_{变化矩阵}$ 进行反向推导，可以认为 $M_{变化矩阵}$ 可能的形式如下：

      $$M_{变化矩阵} = \begin{pmatrix} Near & 0 & 0 & 0 \\ 0 & Near & 0 & 0 \\ 0 & 0 & ? & ? \\ 0 & 0 & -1 & 0 \end{pmatrix} (其中，将第三行前两个位置为0，是因为z的值和x,y无关)$$

      将上面推导出来的矩阵乘以 $\begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix}$ ，结果还是$\begin{pmatrix} x \cdot Near \\ y \cdot Near \\ 未知 \\ -z \end{pmatrix}$，说明 $M_{变化矩阵}$ 符合这种形式

      现在，只需要推导出该变换矩阵的第三行的构成，就能够得到我们的目标： 将透视视锥体变成一个长方体的变换矩阵

      故假设两个未知量分别为 $a,b$，得到：

      $$M_{变化矩阵} = \begin{pmatrix} Near & 0 & 0 & 0 \\ 0 & Near & 0 & 0 \\ 0 & 0 & a & b \\ 0 & 0 & -1 & 0 \end{pmatrix}$$

   2. 接着，将上步推导的 $M_{变化矩阵}$ 代入到 1，2 式中：

      先将 $M_{变化矩阵}$ 代入到1式内：

      $$M_{变化矩阵} \begin{pmatrix} 0 \\ 0 \\ -Near \\ 1 \end{pmatrix} = \begin{pmatrix} Near & 0 & 0 & 0 \\ 0 & Near & 0 & 0 \\ 0 & 0 & a & b \\ 0 & 0 & -1 & 0 \end{pmatrix} \begin{pmatrix} 0 \\ 0 \\ -Near \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ -Near \\ 1 \end{pmatrix}$$

      对上式的结果进行变形：

      $$\because \begin{pmatrix} 0 \\ 0 \\ -Near \\ 1 \end{pmatrix} \times Near = \begin{pmatrix} 0 \\ 0 \\ -Near^2 \\ Near \end{pmatrix} (映射的点不变) \\ \ \\ \therefore \begin{pmatrix} Near & 0 & 0 & 0 \\ 0 & Near & 0 & 0 \\ 0 & 0 & a & b \\ 0 & 0 & -1 & 0 \end{pmatrix} \begin{pmatrix} 0 \\ 0 \\ -Near \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ -Near^2 \\ Near \end{pmatrix}$$

      根据上式即可得到等式：

      $$-a \cdot Near + b = -Near^2$$

      在将 $M_{变化矩阵}$ 代入到2式内：

      $$M_{变化矩阵} \begin{pmatrix} 0 \\ 0 \\ -Far \\ 1 \end{pmatrix} = \begin{pmatrix} Near & 0 & 0 & 0 \\ 0 & Near & 0 & 0 \\ 0 & 0 & a & b \\ 0 & 0 & -1 & 0 \end{pmatrix} \begin{pmatrix} 0 \\ 0 \\ -Far \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ -Far \\ 1 \end{pmatrix}$$

      对上式做相同的变形：

      $$\because \begin{pmatrix} 0 \\ 0 \\ -Far \\ 1 \end{pmatrix} \times Far = \begin{pmatrix} 0 \\ 0 \\ -Far^2 \\ Far \end{pmatrix} (映射的点不变) \\ \ \\ \therefore \begin{pmatrix} Near & 0 & 0 & 0 \\ 0 & Near & 0 & 0 \\ 0 & 0 & a & b \\ 0 & 0 & -1 & 0 \end{pmatrix} \begin{pmatrix} 0 \\ 0 \\ -Far \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ -Far^2 \\ Far \end{pmatrix}$$

      根据上式即可得到等式：

      $$-a \cdot Far + b = -Far^2$$

   3. 对得到的两个二元一次方程求解，得到 $a,b$：

      $$\begin{cases} -a \cdot Near + b = -Near^2 \\ -a \cdot Far + b = -Far^2 \end{cases}$$

      由于 $Far$ 和 $Near$ 已知，故解方程 $a,b$ 可得：

      $$\begin{cases} a = Far + Near \\ b = Far \times Near \end{cases}$$

   最终，我们推导得到了 $M_{变化矩阵}$ 为：

   $$M_{变化矩阵} = \begin{pmatrix} Near & 0 & 0 & 0 \\ 0 & Near & 0 & 0 \\ 0 & 0 & Far + Near & Far \cdot Near \\ 0 & 0 & -1 & 0 \end{pmatrix}$$

2. 将视锥体中心位移到观察空间原点中心

   由于已将透视视锥体转换为了正方体视锥体，可以直接使用正交投影变换得出的结论：将视锥体中心位移到观察空间原点中心

   平移矩阵为：

   $$\begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & \frac{Near+Far}{2} \\ 0 & 0 & 0 & 1 \\ \end{pmatrix}$$

3. 将长方体视锥体的$x,y,z$坐标范围映射到(-1,1)长宽高为2的正方体中

   由于已将透视视锥体转换为了正方体视锥体，因此可以使用正交投影变换的推导过程：
   将长方体视锥体的x,y,z坐标范围映射到(-1,1)长宽高为2的正方体中

   但需要注意的是，透视投影的观察空间中的$x,y,z$和齐次坐标系中$x,y,z$的关系与正交投影不一致，
   这是因为远近裁剪面的宽高的计算方法和正交投影不一致，
   透视投影的观察空间中的$x,y,z$和齐次坐标系中$x,y,z$的关系如下图：

   ​​

   根据这个关系图，可以得到一些转换公式：

   $$\begin{cases} X_齐 = \frac{2}{2 \times Aspect \times Near \times \tan(\frac{FOV}{2})} X_观 \\ Y_齐 = \frac{2}{2 \times Near \times \tan(\frac{FOV}{2})} Y_观 \\ Z_{未取反} = \frac{2}{-Near - (-Far)} Z_观 = \frac{2}{Far - Near} Z_观 \end{cases}$$

   同样，由于要将右手坐标系（观察空间）转换为左手坐标系（裁剪空间），因此要对z分量取反，最终得到公式：

   $$\begin{cases} X_齐 = \frac{1}{Aspect \times Near \times \tan(\frac{FOV}{2})} X_观 \\ Y_齐 = \frac{1}{Near \times \tan(\frac{FOV}{2})} Y_观 \\ Z_{齐} = -\frac{2}{Far - Near} Z_观 \end{cases}$$

   将其转换为矩阵：

   $$\begin{pmatrix} \frac{1}{Aspect \times Near \times \tan(\frac{FOV}{2})} & 0 & 0 & 0 \\ 0 & \frac{1}{Near \times \tan(\frac{FOV}{2})} & 0 & 0 \\ 0 & 0 & -\frac{2}{Far - Near} & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix}$$

以上三步得到了三个矩阵，将其合并为一个矩阵，得到最终的 透视投影空间 转换到 齐次坐标裁剪空间 的变换矩阵

$$\begin{pmatrix} \frac{1}{Aspect \times Near \times \tan(\frac{FOV}{2})} & 0 & 0 & 0 \\ 0 & \frac{1}{Near \times \tan(\frac{FOV}{2})} & 0 & 0 \\ 0 & 0 & -\frac{2}{Far - Near} & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & \frac{Near+Far}{2} \\ 0 & 0 & 0 & 1 \\ \end{pmatrix} \begin{pmatrix} Near & 0 & 0 & 0 \\ 0 & Near & 0 & 0 \\ 0 & 0 & Far + Near & Far \cdot Near \\ 0 & 0 & -1 & 0 \end{pmatrix} \\ = \begin{pmatrix} \frac{1}{Aspect \cdot \tan(\frac{FOV}{2})} & 0 & 0 & 0 \\ 0 & \frac{1}{\tan(\frac{FOV}{2})} & 0 & 0 \\ 0 & 0 & -\frac{Far + Near}{Far - Near} & -\frac{2 Far\cdot Near}{Far - Near} \\ 0 & 0 & -1 & 0 \\ \end{pmatrix}$$

注意，由该矩阵转换出来的四维齐次坐标**$(x',y',z',w')$** ，其 $w'$ 很有可能不是1，
这时我们可以对坐标除以 $w'$ 标量，使其为1，这样得到的 $\frac{x'}{w},\frac{y'}{w},\frac{z'}{w}$ ，如果在 $(-1,1)$ 内就是不需要裁剪的
或者我们可以直接判断 $x',y',z'$ 是否在 $(-w',w')$ 内，如果是就不需要裁剪

‍