US2S1L18——裁剪空间变换的意义
知识回顾
裁剪空间变换的意义
我们之所以要将观察空间中的顶点等信息变换到裁剪空间中主要意义,
其实就是为了让我们可以更通用、便捷的来进行裁剪工作。
因为如果直接使用视锥体定义的空间来进行裁剪,那不同的视锥体就需要不同的处理过程,
比如正交摄像机的 Size、Near、Far 等参数,透视摄像机中的 FOV、Near、Far 等参数
他们决定了视锥体的体积大小会各不相同,而且对于透视投影的视锥体来说,判断顶点是否在其范围内相对较麻烦。
因此前辈们就制定了裁剪空间这一规则,让我们可以更容易的完成裁剪工作,这也是该变换的意义所在
如何决定顶点是否被裁剪
对观察空间下的顶点进行裁剪空间变换后,得到的点(x,y,z,w):
-
正交摄像机的裁剪判断方式:
⎩⎨⎧−1≤x≤1−1≤y≤1−1≤z≤1(位于此范围内就是不需要裁剪的)
-
透视摄像机的裁剪判断方式
⎩⎨⎧−w≤x≤w−w≤y≤w−w≤z≤w(位于此范围内就是不需要裁剪的)
首先我们还是之前用于举例的顶点来说明
模型空间下的顶点坐标为(0.63, 0.84, -0.04)
当模型进行2倍缩放,又进行(0, 45, 0)的旋转,然后再进行(5 ,0, 5)的平移后
该顶点的世界空间下的坐标为(5.834, 1.68, 4.052)
摄像机的轴向和坐标为
1
2
3
4
| print(this.transform.right);
print(this.transform.up);
print(-this.transform.forward);
print(this.transform.position);
|
转换到观察空间后的坐标为(4.562, 0.659, -7.722, 1)
假设屏幕宽高比为:
如果是正交摄像机,参数为:
将数据代入到正交投影变换矩阵内,得到:
Aspect×Size10000Size10000−Far−Near2000−Far−NearNear+Far14.5620.659−7.7221=0.5132250.12580.4922841
显然,这个点的 x,y,z 都在(−1,1)的范围内,故不需要裁剪
如果是正交摄像机,参数为: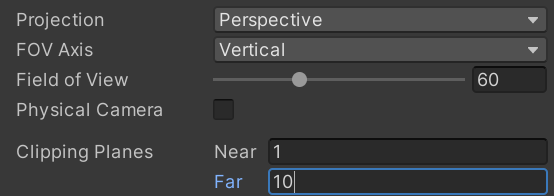
将数据代入到透视投影变换矩阵内,得到:
Aspect⋅tan(2FOV)10000tan(2FOV)10000−Far−NearFar+Near−100−Far−Near2Far⋅Near04.5620.659−7.7221=4.4461.1767.21427.722
要注意,此时我们求出来的坐标其 w′ 不为1,我们必须要除以 w′ 标量使其为1,这样得出来的坐标才是三维空间下真正的坐标
4.4461.1767.21427.722÷7.722=0.57570.1520.93421
显然,这个点的 x,y,z 都在(−1,1)的范围内,故不需要裁剪




