US2S1L19——屏幕空间变换
知识回顾
-
在渲染管线中,顶点、法线等相关模型数据会经过以下的空间变换
模型空间 → 世界空间 → 观察空间 → 裁剪空间 → 屏幕空间
-
坐标空间变换规则一般有两种
-
方式一:通用的坐标空间变换规则(存在缩放时,轴向单位向量*缩放因子)
Ms−f=kx0000ky0000kz00001∣Xs∣0∣Ys∣0∣Zs∣0∣Os∣1
-
方式二:认为一开始模型坐标空间和世界坐标空间重合,模型发生缩放、旋转、平移变换时,模型空间下的点和向量也应该发生相同的变换
-
观察空间到裁剪空间变换要分情况考虑
-
摄像机为正交投影时:
- 将视锥体中心位移到观察空间原点中心
- 将长方体视锥体的xyz坐标范围映射到(-1,1)长宽高为2的正方体中
正交投影变换矩阵为:
Aspect×Size10000Size10000−Far−Near2000−Far−NearNear+Far1
-
摄像机为透视投影时:
- 将透视视锥体变成一个长方体
- 将视锥体中心位移到观察空间原点中心
- 将长方体视锥体的xyz坐标范围映射到(-1,1)长宽高为2的正方体中
透视投影变换矩阵为:
Aspect⋅tan(2FOV)10000tan(2FOV)10000−Far−NearFar+Near−100−Far−Near2Far⋅Near0
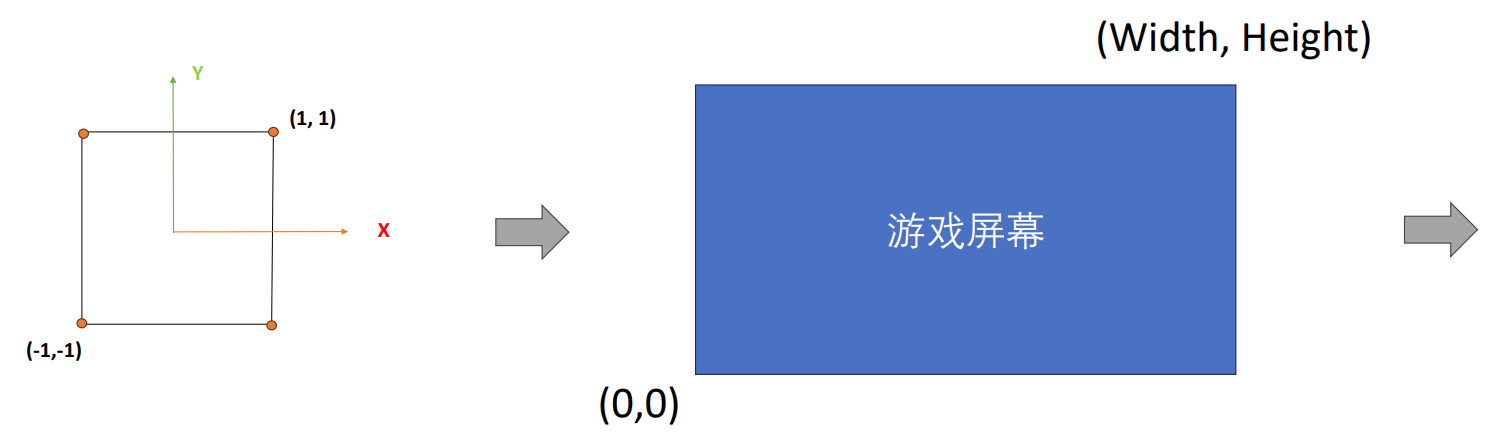
屏幕空间变换
-
屏幕空间的意义
屏幕空间中对应的位置信息是真正的像素位置
-
屏幕空间变换指什么
将模型空间中的点或向量从裁剪空间中变换到屏幕空间中
它是顶点变换的第四步,就是将 数据 从裁剪空间 → 屏幕空间 进行变换
-
如何进行屏幕空间变换
⎩⎨⎧X屏=2⋅WclipWidth⋅Xclip+2Width Y屏=2⋅WclipHeight⋅Yclip+2Height
- Z:WclipZclip 会被存入深度缓冲中(不同硬件商存储方式可能不同),之后用于 深度测试 等计算,关于深度测试,可见:逐片元操作中的深度测试流程
- W:Wclip 也会被保留下来,用于之后进行一些计算才做,例如透视校正插值(详细可参考:图形学 - 关于透视矫正插值那些事 - 知乎)
屏幕空间的意义
屏幕空间(Screen Space)是计算机图形学中的概念
指渲染结果在屏幕上显示的坐标空间三维坐标经过一系列转换后会转换到最终的二维屏幕坐标空间中
使得图像可以在屏幕上进行展示。
屏幕空间的主要意义是屏幕空间中对应的位置信息是真正的像素位置,而不是虚拟的三维坐标。
有了相对屏幕空间的坐标位置,才能准确的控制屏幕上像素点的显示效果
屏幕空间中的注意事项
在Unity中,屏幕空间左下角为像素坐标(0,0)点
屏幕空间右上角为像素坐标(分辨率宽 Screen.width,分辨率高 Screen.height)

屏幕空间变换指什么
本课程中的屏幕空间变换指的主要是将模型空间中的点或向量从裁剪空间中变换到屏幕空间中
它是顶点变换的第四步,就是将 顶点坐标数据 从裁剪空间 → 屏幕空间 进行变换
从图中我们可以看到,主要是**将三维坐标(x,y,z)中的x,y分量映射到屏幕上,而z分量一般会被用于深度缓冲**,之后用于深度测试等(决定是否被遮挡等)
屏幕空间变换,可以说是所有空间变换中最简单的一步,
我们只需要将齐次裁剪空间(x,y,z范围在-1到1之间,长度为2的正方体)中的顶点映射到屏幕坐标即可。
我们只需要找到他们的映射关系即可。
首先我们通过 上节课 知道,正交投影中 w 分量为1,透视投影中 w 分量可能为任一数,
我们首先需要进行透视除法,保证裁剪空间中点的数据表达在齐次裁剪空间的范围内。
即,假设 裁剪空间中的点为(Xclip,Yclip,Zclip,Wclip)进行透视除法:
(WclipXclip,WclipYclip,WclipZclip,WclipWclip)
对于正交投影来说 W 值为1,所以除以1后,x,y,z也不会改变
对于透视投影来说 W 值为任一值,所以除以 W 后,X,Y,Z的范围将在-1到1之间,W为1
如何进行屏幕空间变换
找到齐次裁剪空间和屏幕空间的映射关系,主要就是找到直线的斜率
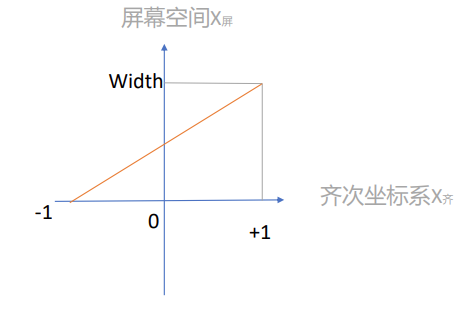
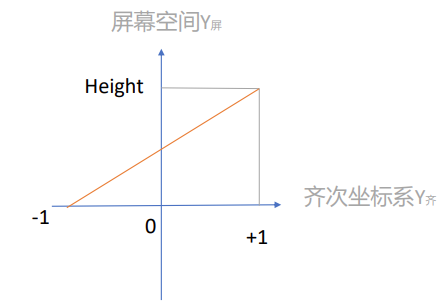
于是得到:
⎩⎨⎧X屏=2Width×X齐+2Width Y屏=2Height×Y齐+2Height
因为存在透视除法,因此上述等式可以转换为:
⎩⎨⎧X屏=2Width×WclipXclip+2Width=2⋅WclipWidth⋅Xclip+2Width Y屏=2Height×WclipYclip+2Height=2⋅WclipHeight⋅Yclip+2Height
那么裁剪空间中的 z,w 会如何处理呢:
- Z:WclipZclip 会被存入深度缓冲中(不同硬件商存储方式可能不同),之后用于深度测试等计算(TODO)
- W:Wclip 也会被保留下来,用于之后进行一些计算才做,例如透视校正差值(TODO)
举例:
首先我们还是之前用于举例的顶点来说明
-
模型空间下的顶点坐标为(0.63, 0.84, -0.04)

-
当模型进行2倍缩放,又进行(0,45,0)的旋转,然后再进行(5,0,5)的平移后
该顶点的世界空间下的坐标为(5.834, 1.68, 4.052)
-
摄像机的轴向和坐标为
1
2
3
4
| print(this.transform.right);
print(this.transform.up);
print(-this.transform.forward);
print(this.transform.position);
|
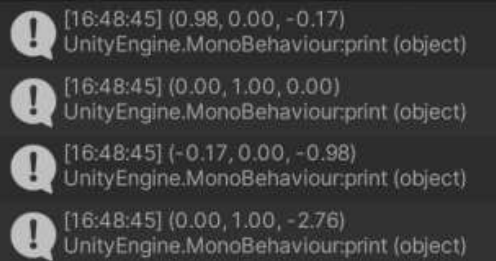
转换到观察空间后的坐标为(4.562, 0.679, -7.722, 1)
-
转换到裁剪空间后的坐标为
- 正交摄像机:(0.513225, 0.1358, 0.492284, 1)
- 透视摄像机:(4.446, 1.176, 7.2142, 7.722)
-
转换到屏幕空间:
假设屏幕分辨率为 1920*1080,
将 x,y 数据代入到下式:
⎩⎨⎧X屏=2⋅WclipWidth⋅Xclip+2Width Y屏=2⋅WclipHeight⋅Yclip+2Height
得到屏幕坐标:
- 屏幕坐标(正交摄像机):(1452.696, 613.332)
- 屏幕坐标(透视摄像机):(1512.7272, 622.237)







