US3S2L4——凹凸纹理基本概念

纹理知识回顾

单张纹理是模型的“皮”，它决定了模型的颜色表现，
在建模时通过纹理隐射技术将顶点和纹理图片建立联系，在模型数据中记录顶点对应的UV坐标，
进行Shader开发时，利用UV坐标即可从纹理图片中取出对应位置的颜色给片元“上色”

凹凸纹理

纹理除了可以用来进行 颜色映射 外，另外一种常见的应用就是进行 凹凸映射
凹凸映射的目的是使用一张纹理来修改模型表面的法线，让我们不需要增加顶点，而让模型看起来有凹凸效果。

原理：光照的计算都会利用法线参与计算，决定最终的颜色表现效果。
那么在 计算 “假” 凹凸面时，使用“真”凹凸面的法线 参与计算，呈现出来的效果可以以假乱真

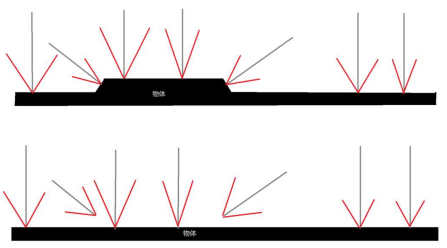
左图是真实凹凸表面的光线，右图是不使用真凹凸表面的光线，
想要在非凹凸面上体现凹凸感，就需要通过法线改变光线方向，通过光照模拟出凹凸感

凹凸纹理最大的作用就是让模型可以 在不添加顶点（不增加面）的情况下
让模型看起来同样充满细节（凹凸感），是一种视觉上的“欺骗”技术

下图就是在凹凸纹理的运用，通过一张凹凸纹理改变光照效果，让模型的表面看起来凹凸不平

要进行凹凸映射，目前有两种主流方式：

高度纹理贴图：RGB都存储高度值，表现为一张灰度图，由于需要更多额外计算，我们一般不使用
法线纹理贴图：RGB分别存储法线的XYZ值，有相对模型空间（彩色）和切线空间（蓝色）两种法线贴图

切线空间法线贴图虽然要产生额外计算，但是能让法线贴图更加的通用，灵活，因此纹理贴图常使用 切线空间法线贴图

通过高度纹理或法线纹理在不添加顶点（不增加面）的情况下让模型看起来同样充满细节（凹凸感）
原理：计算 “假” 凹凸面时，使用 “真” 凹凸面的法线参与计算

高度纹理贴图一般简称高度图，它存储了模型表面上每个点的高度信息。
通常它使用灰度图像，其中不同灰度值表示不同高度。
较亮区域通常对应较高的点，较暗的区域对应较低的点。

它主要用于模拟物体表面的位移。

存储规则：图片中的某一个像素点的 RGB 值是相同的，都表示高度值，A值一般情况下为1。高度值范围一般为0~1，0代表最低，1代表最高

我们在使用凹凸纹理时，一般都会使用法线纹理贴图

法线纹理贴图一般简称法线贴图或法线纹理，它存储了模型表面上每个点的法线方向。

存储规则：图片中的 RGB 值分别存储法线的X、Y、Z分量值，A值可以用于存储其他信息，比如材质光滑度等。

由于法线纹理贴图是我们之后实现“凹凸感”的主要方式，因此我们需要更详细的了解它的存储规则

由于法线方向 XYZ 分量范围在 $[-1,1]$ 之间，而像素颜色 RGB 分量范围在 $[0,1]$ 之间，因此我们需要做一个映射计算

存储图片时： $像素颜色分量 = (法线方向分量 + 1) \div 2$

因此当我们取出像素分量使用时需要进行逆运算

读取数据时： $法线方向分量 = 像素颜色分量 \times 2 - 1$

法线纹理贴图中主要存储法线信息，而法线信息其实就是个方向向量，而方向向量就得有相对坐标系
因此，法线贴图的存储方式按相对坐标系有两种方式：

模型数据中自带的法线数据，是定义在模型空间中的，因此最直接的存储法线贴图数据的方式，就是存储基于模型空间下的法线信息。

注意：模型数据中的法线数据是 “真” 数据，也就是基于模型的真实存在的面得到的法线信息
法线贴图中对的法线数据是 “假” 数据，是通过人为添加或修改的法线数据，原本模型的面上不存在这些人为添加法线对应的凹凸面

如下图所示，由于模型空间中每个点存储的法线方向是各式各样的，比如：

因此，基于模型空间的法线纹理一般是五颜六色的，这种法线纹理贴图数据取出来直接参与 Shader 计算即可
对于不需要变形的静态物体来说非常有用，因为法线方向不会随着物体的变化而变化。

虽然基于模型空间的法线纹理贴图看起来很符合计算需求，但是在实际开发时，美术同学给到我们的法线贴图一般都是基于切线空间的

每个顶点都有自己的切线空间，它的 XYZ 轴及原点代表的信息分别如下：

在切线空间下，如果该顶点的法线不变化（不需要“凹凸感”）
那么它的坐标是 $(0,0,1)$ ，因为在切线空间下，Z 轴就是原法线方向，因此：

法线 $(0,0,1)$ 映射到像素后 $像素分量 = (法线分量 + 1) \div 2$ 是 $(0.5,0.5,1)$ 也就是浅蓝色

这个浅蓝色就是切线空间下法线贴图存在大片蓝色的原因，因为大部分顶点的法线和模型本身法线是一致的，只有凹凸部分的颜色才会有些许差异

这种法线纹理贴图数据取出来后需要进行坐标空间转换，再参与 Shader 计算
由于切线空间下的法线信息与模型的局部坐标系无关，所以可以在不同的物体上重复使用相同的纹理

之所以在实际开发时要使用切线空间下的法线贴图，原因有以下几点：

等等