US3S2L5——法线贴图的计算方式
US3S2L5——法线贴图的计算方式
回顾知识:
转置矩阵:将原始矩阵的行和列互换得到的新矩阵,假设矩阵为 ,那 的转置矩阵一般写为
正交矩阵:一个方阵和它的转置矩阵相乘为单位矩阵,就是正交矩阵:,正交矩阵的逆矩阵就是其转置矩阵
基础变换矩阵的构成规则:
一个能表示旋转缩放,平移的 矩阵的基本构成规则为:
- 矩阵的 部分用于表示旋转和缩放变换
- 矩阵的 部分用于表示平移
- 矩阵的 部分始终为零矩阵
- 矩阵的 右下角元素 始终为 1
若变换矩阵用来变换矢量,可以直接使用 部分,因为矢量不受平移影响
坐标空间的变换规则:
从子坐标空间到父坐标空间的变换矩阵:
其中, 是子坐标系的三个轴向的方向向量(不一定是单位向量), 是子坐标空间的原点在父坐标空间上的坐标
对于存在缩放的子坐标空间,需要用 轴向的 单位向量 对应轴 的缩放因子,详见:使用坐标变换规则进行模型空间变换
从父坐标空间到子坐标空间的变换矩阵:
法线贴图两种主流计算方式
在上节课提到,想要实现凹凸效果,主要就是使用基于切线空间的法线贴图中的法线信息参与到光照计算中
而在计算光照模型时,通常会有两种选择:
- 在切线空间下进行光照计算,需要把光照方向、视角方向变换到切线空间下参与计算
- 在世界空间下进行光照计算,需要把法线方向变换到世界空间下参与计算
这两者的优缺点如下:
从效率上来说:
- 在切线空间中计算,效率更高, 因为可以在顶点着色器中就完成对光照、视角方向的矩阵变换,计算量相对较小。
(矩阵变换在顶点着色器中计算) - 在世界空间中计算,效率较低, 由于需要对法线贴图进行采样,所以变换过程必须在片元着色器中实现,我们需要在片元着色器中对法线进行矩阵变换。
(矩阵变换在片元着色器中计算)
从全局效果上来说:
- 在切线空间中计算,对全局效果的表现可能会不够准确, 在处理一些列如镜面反射、环境映射效果时表现效果可能不够准确
- 在世界空间中计算,对全局效果的表现更准确, 可以更容易的应用于全局效果的计算
因此我们在选择使用哪种计算方式时,主要考虑:
若没有全局效果要求,我们优先使用在切线空间下进行光照计算,因为它效率较高
反之,我们选择在世界空间下计算,具体使用哪种还是以项目的实际情况决定
在切线空间下计算凹凸光照
在切线空间下进行光照计算,需要把光照方向、视角方向变换到切线空间下参与计算
-
关键点:计算模型空间到切线空间的变换矩阵
变换矩阵为子到父的 逆矩阵
由于我们主要用 变换矩阵来进行矢量的变换 而非点的变换,因此可以变为 矩阵:
而 x、y、z 轴分别为 切线空间中顶点的切线、副切线、法线, 已知切线、法线(从模型数据中可以获取),副切线为切线、法线的叉乘结果
而3个轴为相互垂直的单位向量,因此可以推出 是正交矩阵
因此该变换矩阵的逆矩阵为其转置矩阵 ,它就是模型空间到切线空间的变换矩阵
-
其他用到的核心知识
内置函数:
- 得到模型空间光的方向:
ObjSpaceLightDir(模型空间顶点坐标) - 得到模型空间视角方向:
ObjSpaceViewDir(模型空间顶点坐标)
得到 光方向 和 视角方向 相对于模型空间的数据表达后
再与 模型空间到切线空间的变换矩阵 进行运算
即可将他们转换到 切线空间下 参与后续计算 - 得到模型空间光的方向:
在世界空间下计算凹凸光照
在世界空间下进行光照计算,需要把法线方向变换到世界空间下参与计算
-
关键点:计算切线空间到世界空间的变换矩阵
变换矩阵为子到父的 逆矩阵
由于我们主要用 变换矩阵来进行矢量的变换 而非点的变换,因此可以变为 矩阵:
而 x、y、z 轴分别为切线空间中顶点的切线、副切线、法线,我们只需要得到3个轴相对于世界空间的向量表达,即可得到该变换矩阵以上三轴的计算方法如下:
- 法线从模型空间到世界空间 :
UnityObjectToWorldNormal(模型空间法线数据) - 切线从模型空间到世界空间 :
UnityObjectToWorldDir(模型空间切线数据) - 世界空间的副切线 :用上面计算的结果叉乘即可
由这三个向量组成最终的切线空间到世界的空间的变换矩阵:
- 法线从模型空间到世界空间 :
关键知识点补充
-
模型空间下的切线数据
模型数据中的切线数据为
float4 类型的(四维向量),其中的w 表示副切线的方向
用法线和切线叉乘得到的副切线方向可能有两个(如下图的两个方向的灰色线),用切线数据中的w与之相乘确定副切线方向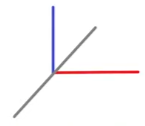
-
Unity 当中的法线纹理类型
当我们把纹理类型设置为 Normal map(法线贴图)时,
我们可以使用Unity提供的内置函数UnpackNormal来得到正确的法线方向。
该函数内部不仅可以进行 的逆运算,
还会进行解压运算(Unity 会根据不同平台对法线纹理进行压缩)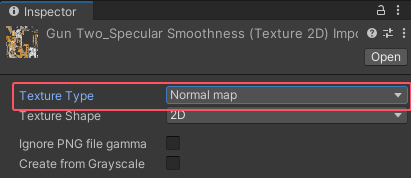
1
float3 tangentNormal = UnpackNormal(packedNormal); // 将颜色数据逆运算并解压缩,得到切线空间下法线数据
-
法线纹理属性命名一般为
_BumpMap(凸块贴图),
并声明一个我们还会声明一个名为_BumpScale(凸块缩放))的float属性,它主要用于控制凹凸程度当它为 0 时,表示没有法线效果,法线的影响会被消除
当它为 1 时,表示使用法线贴图中的原始法线信息,没有缩放
我们可以根据实际需求调整它的值,来达到视觉上令人满意的效果 -
如果使用的凹凸纹理不是法线纹理,而是高度纹理(灰度图)
我们需要进行如下设置:
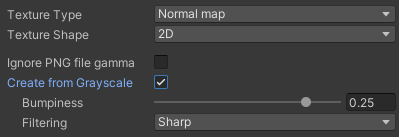
图片类型设置为 Normal map(法线贴图)并勾选 Create from Grayscale(从灰度创建)
这样我们就可以把高度纹理当成切线空间下的法线纹理处理了多出的参数分别为:
-
Bumpiness(颠簸值):控制凹凸程度
-
Filtering(过滤模式):决定凹凸程度的算法
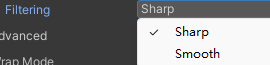
- Sharp:滤波生成法线
- Smooth:平滑的生成法线
-
