CS4L25——插入排序

插入排序

插入排序（insertion sort）是一种简单的排序算法，它的工作原理与手动整理一副牌的过程非常相似。

将待排序数组分为两个区域，一个是排序区，另一个是未排序区，用一个索引值做分水岭，
未排序区元素与排序区元素比较，插入到合适位置，直到未排序区清空

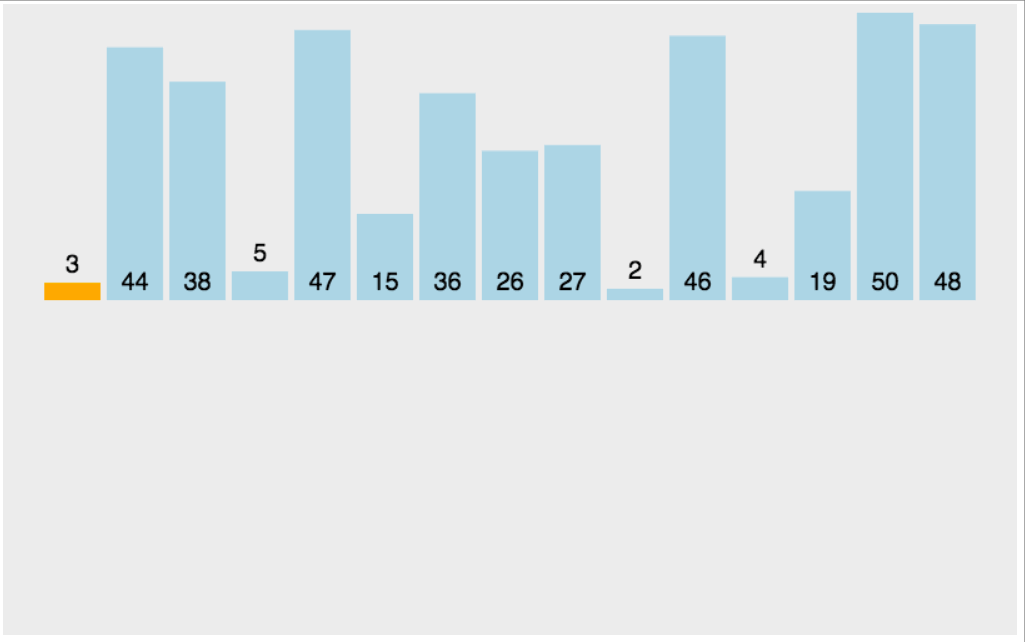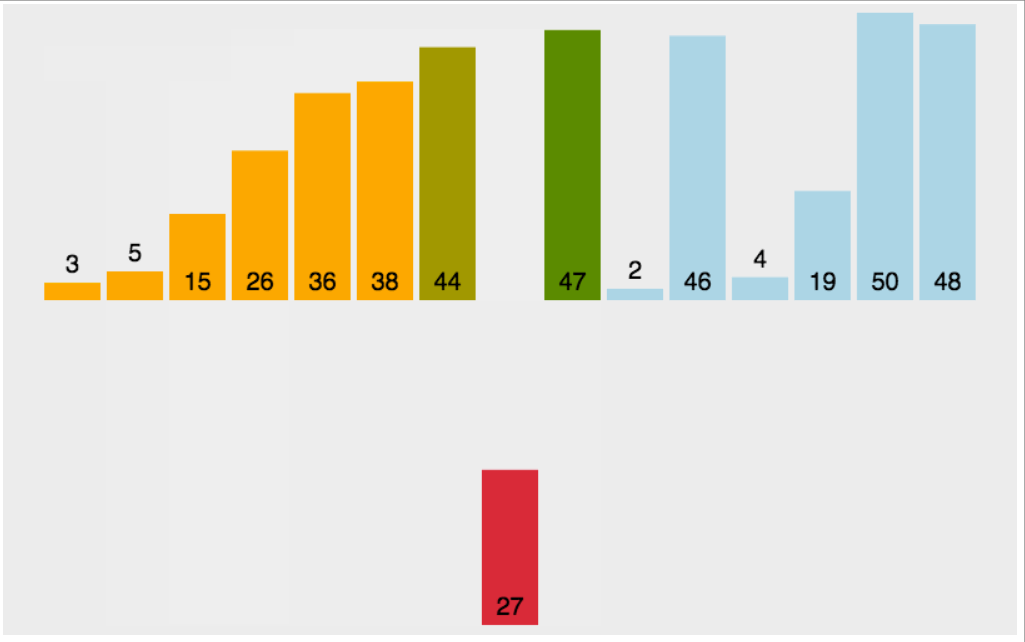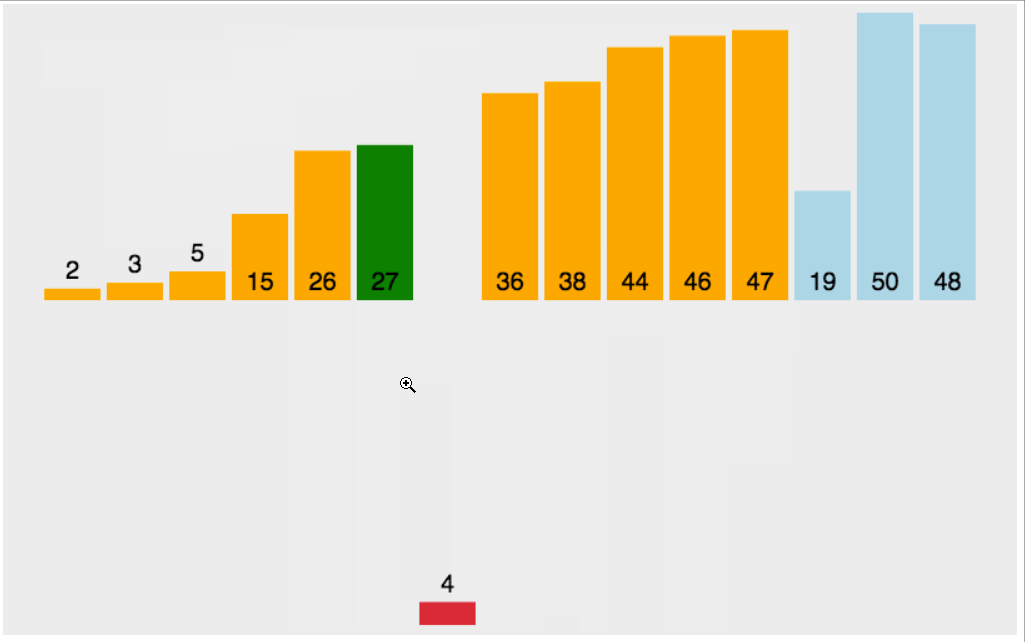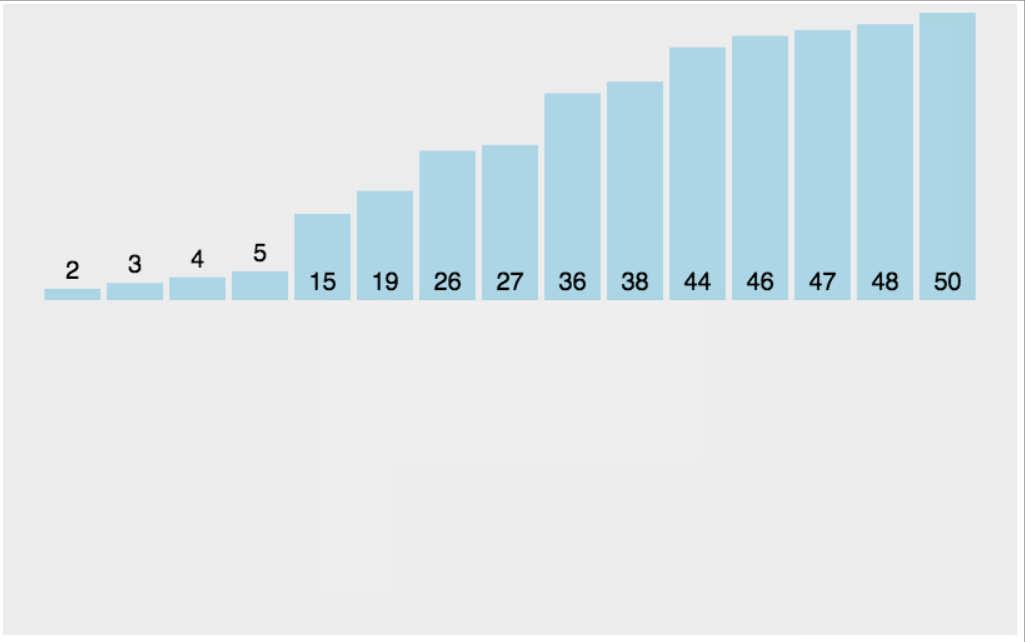
插入排序动图

插入算法的实现

前提规则：

排序开始前：首先认为第一个元素在排序区中，其他所有元素在未排序区中
排序开始后：每次将未排序区第一个元素取出和，排序区中元素比较从后往前，满足条件（较大或者较小），则排序区中元素往后移动一个位置

注意：所有数字都在一个数组中，所谓的两个区域是一个分水岭索引

static void InsertionSort(int[] nums)
{
    // 第一步，取出未排序区的所有元素进行比较，i = 1的原因：默认第一个元素就在排序区
    for (int i = 1; i < nums.Length; i++)
    {
        // 第二步
        int sortIndex = i - 1;      // 取出排序区的最后一个元素索引
        int noSortNum = nums[i];    // 取出未排序区的第一个元素
        // 第三步，在排序区进行比较，将排序区中比取出元素大的值向后移动，并确定插入索引
        while (sortIndex >= 0 && nums[sortIndex] > noSortNum)
        {
            nums[sortIndex + 1] = nums[sortIndex];
            --sortIndex;
        }
        // 最终插入数字
        nums[sortIndex + 1] = noSortNum;
    }
}

static void Main(string[] args)
{
    int[] arr = new int[] { 8, 7, 1, 5, 4, 2, 6, 3, 9 };
    Console.Write("未排序：");
    for (int i = 0; i < arr.Length; i++)
    {
        Console.Write($"{arr[i]}, ");
    }
    Console.Write("\n");
    InsertionSort(arr);
    Console.Write("已排序：");
    for (int i = 0; i < arr.Length; i++)
    {
        Console.Write($"{arr[i]}, ");
    }
    Console.Write("\n");
}

两层循环的原因：

第一层：依次取出未排序区的元素进行排序
第二层：找到想要插入的位置

为什么第一层循环从 1 开始遍历的原因：插入排序的关键是分两个区域，已排序区和未排序区，默认第一个元素在已排序区

为何使用 while 循环：满足条件（未找到插入位置）才比较，否则证明插入位置已经确定，不需要继续循环

为什么可以直接往后移位置：每轮未排序数已记录，最后一个位置不怕会丢失

为什么确定位置后，是放在 sortIndex + 1 的位置：当循环停止时，插入位置是停止循环的索引 + 1处

输出：

1 2	未排序：8, 7, 1, 5, 4, 2, 6, 3, 9, 已排序：1, 2, 3, 4, 5, 6, 7, 8, 9,

算法特性

时间复杂度为 ** $O(n^2)$ ** 、自适应排序：在最差情况下，每次插入操作分别需要循环 $n−1、n−2、…、2、1$ 次，求和得到 $(n−1)n/2$ ，
因此时间复杂度为 $O(n^2)$ 。在遇到有序数据时，插入操作会提前终止。当输入数组完全有序时，插入排序达到最佳时间复杂度 $O(n)$ 。
空间复杂度为 ** $O(1)$ ** 、原地排序：指针 $i$ 和 $j$ 使用常数大小的额外空间。
稳定排序：在插入操作过程中，我们会将元素插入到相等元素的右侧，不会改变它们的顺序。

插入排序的优势

插入排序的时间复杂度为 $O(n^2)$ ，而我们即将学习的快速排序的时间复杂度为 $O(n\log⁡n)$ 。
尽管插入排序的时间复杂度更高，但在数据量较小的情况下，插入排序通常更快。

这个结论与线性查找和二分查找的适用情况的结论类似。
快速排序这类 $O(n\log⁡n)$ 的算法属于基于分治策略的排序算法，往往包含更多单元计算操作。
而在数据量较小时， $n^2$ 和 $n\log⁡n$ 的数值比较接近，复杂度不占主导地位，每轮中的单元操作数量起到决定性作用。

实际上，许多编程语言（例如 Java）的内置排序函数采用了插入排序，大致思路为：对于长数组，采用基于分治策略的排序算法，例如快速排序；对于短数组，直接使用插入排序。

虽然冒泡排序、选择排序和插入排序的时间复杂度都为 $O(n^2)$ ，
但在实际情况中，插入排序的使用频率显著高于冒泡排序和选择排序，主要有以下原因：

冒泡排序基于元素交换实现，需要借助一个临时变量，共涉及 3 个单元操作；
插入排序基于元素赋值实现，仅需 1 个单元操作。因此，冒泡排序的计算开销通常比插入排序更高。
选择排序在任何情况下的时间复杂度都为 $O(n^2)$ 。如果给定一组部分有序的数据，插入排序通常比选择排序效率更高。
选择排序不稳定，无法应用于多级排序。